Золотая середина: двойную сплошную покрасят в желтый | Статьи
Для обозначения линий, разделяющих встречные полосы движения на трассах, нужно использовать желтую разметку. Такую рекомендацию в рамках проекта «Безопасные и качественные автодороги» региональным властям дал Минтранс. Предполагается, что желтая разметка будет видна лучше нынешней белой. Пока что выезд на встречную полосу — одна из главных причин ДТП в России.
Рекомендация использовать желтую разметку «на двух- и трехполосных дорогах для обозначения линий, разделяющих встречные направления движения» в числе других мер приложена к письму за подписью замглавы Минтранса Иннокентия Алафинова губернаторам о реализации нацпроекта «Безопасные и качественные дороги» (есть у «Известий»). Ранее власти субъектов уже подготовили региональные планы работы в этом направлении. Федеральный чиновник просит их скорректировать исходя из рекомендаций министерства.
Пункт о желтой разметке включен по предложению Главного управления по обеспечению безопасности дорожного движения МВД России «в целях повышения безопасности на дорогах и является не обязательным требованием, а рекомендацией», сказали «Известиям» в Минтрансе.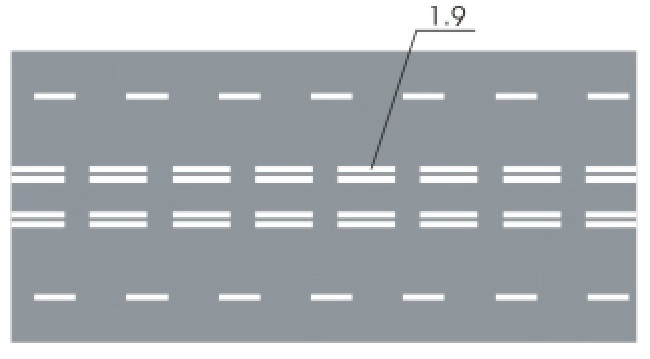
Как писали «Известия», весной Росавтодор проводил эксперимент по использованию желтой разметки в Мурманской области, Карелии и Краснодарском крае. Испытания показали, что число ДТП снижается на 30%, рассказали «Известиям» в МВД. Желтые линии особенно хорошо видны зимой на заснеженной проезжей части, отметили в ведомстве.
В Росавтодоре подтвердили информацию и объясняли, что идею цветной разметки заимствовали в странах Скандинавии.
Пока что выезд на полосу встречного движения — одна из основных причин аварий, указано в оперативном обзоре за девять месяцев Научного центра безопасности дорожного движения при МВД. За январь–сентябрь произошло 9,5 тыс. таких ДТП (9% от общего числа), но тяжесть их последствий считается самой высокой. Только за девять месяцев этого года в авариях из-за выезда на встречную полосу погибло 3,1 тыс. человек и были ранены 17,6 тыс. граждан.
ГОСТ, допускающий использование желтой и синей разметки, вступил в силу 1 июня. По документу все основные виды дорожных линий, разделяющих потоки и полосы движения (одинарная и двойная сплошная, прерывистая, комбинация прерывистой и сплошной), могут быть как белого, так и желтого цвета. Синими могут быть прерывистые линии, используемые для направления движения на перекрестках.
Синими могут быть прерывистые линии, используемые для направления движения на перекрестках.
Инициативу Минтранса можно поддержать, если ее необходимость будет обоснована ведомством, сказал «Известиям» губернатор Тульской области Алексей Дюмин.
Опыт использования желтой разметки со светоотражающими элементами в скандинавских странах говорит о возможности снизить аварийность в разы, отметил директор по закупкам транспортных услуг FM Logistic Эдуард Миронов. Однако это не единственный способ предотвратить выезд на встречную полосу или обочину, отметил он. Например, в США распространена шумовая разметка: выпуклые элементы на дороге вызывают вибрацию и гудение в автомобиле и не позволяют съехать в сторону без усилий. В опасной ситуации такая система позволяет разбудить заснувшего водителя.
Мера, которая значительно сократит смертельные исходы в ДТП, — это установка бетонных либо проволочных ограждений, разделяющих встречные направления, уверена директор по перевозкам и эксплуатации транспорта компании Intertransavto (ITA) Виктория Роговенко. По ее мнению, изменение цвета разметки значительно не отразится на статистике аварийности.
По ее мнению, изменение цвета разметки значительно не отразится на статистике аварийности.
«Безопасные и качественные дороги» — один из 12 нацпроектов, разработанных во исполнение новых майских указов президента. Он призван снизить смертность в ДТП в 3,5 раза, до четырех случаев на 100 тыс. населения, к 2024 году. Нацпроект предлагает, например, довести до нормативного состояния половину региональных дорог и 85% трасс в крупных городах и установить 10 тыс. новых камер для фиксации нарушений. Сейчас документ на стадии утверждения.
ЧИТАЙТЕ ТАКЖЕ
Жизнь водителей заиграет новыми красками – Газета Коммерсантъ № 43 (6281) от 15.03.2018
Новый ГОСТ дорожной разметки, утвержденный Росстандартом, содержит ряд нововведений, которые вскоре станут заметны всем участникам движения. В частности, зоны, где запрещен обгон, впервые будут обозначены желтыми полосами, а полосы движения на перекрестках — синими. Новые обозначения на асфальте не дадут пропустить водителям зону разворота или запрета выезда на перекресток. Разработчики нового стандарта пояснили “Ъ”, что постарались сделать разметку максимально удобной для участников движения. Нововведения вступают в силу 1 июня 2018 года.
Разработчики нового стандарта пояснили “Ъ”, что постарались сделать разметку максимально удобной для участников движения. Нововведения вступают в силу 1 июня 2018 года.
Приказом Росстандарта №81-ст утвержден новый ГОСТ Р 51256–2018 «Технические средства организации дорожного движения. Разметка дорожная. Классификация. Технические требования». Документ, который готовился по заказу Росавтодора, вступает в силу 1 июня 2018 года.
Согласно стандарту, все основные виды дорожной разметки, разделяющей потоки и полосы движения (одинарная и двойная сплошная, прерывистая, комбинация прерывистой и сплошной) могут быть как белого, так и желтого цвета. До сих пор желтая маркировка применялась только для обозначения зон запрета стоянки. Синими могут стать прерывистые линии, используемые для направления движения на перекрестках.
Вводится ряд новых обозначений, которые наносятся на асфальт: знак, обозначающий станцию зарядки электромобилей, разметка типа «вафельница» (зона, в которую запрещено въезжать во время затора на перекрестке). Последняя в качестве эксперимента, отметим, уже применяется на 30 перекрестках в Москве, новым ГОСТом она будет легализована. Стандартом впервые предусмотрена стрелка, обозначающая зону разворота,— в старом ГОСТе ее не было, были только стрелки поворотные.
Последняя в качестве эксперимента, отметим, уже применяется на 30 перекрестках в Москве, новым ГОСТом она будет легализована. Стандартом впервые предусмотрена стрелка, обозначающая зону разворота,— в старом ГОСТе ее не было, были только стрелки поворотные.
Новый ГОСТ принят в рамках приведения документации в соответствие с техрегламентом Таможенного союза 2011 года «Безопасность автодорог» и ПДД, рассказал “Ъ” разработчик стандарта гендиректор центра инженерно-технических исследований (ЦИТИ) «Дорконтроль» Владислав Свежинский. Разметка желтого цвета, пояснил он, позволяет «улучшить ее видимость», особенно в регионах, где обильно выпадает снег. Синяя разметка, говорит господин Свежинский, будет применяться для обозначения платной и бесплатной парковки, но конкретные правила применения закрепит в новой редакции другого ГОСТа, который сейчас также перерабатывается. Любопытно, что разметка 1.7 (синяя по новому ГОСТу) могла использоваться в качестве разметки парковочных зон до июля 2017 года: в ПДД были внесены изменения, и эту опцию убрали.
Замначальника ситуационного центра московского ЦОДД Андрей Мухортиков нововведения поддержал, отметив важность разметки, обозначающий разворот. «До сих пор под знаком «Разворот» размещалась стрелка с поворотом, что, конечно, путало водителей,— рассказал он.— Логика появления синих линий понятна, она уже давно применяется в Европе для обозначения парковочных зон». Cплошные осевые линии, обозначения обочин, влияющие на безопасность, должны быть белыми, желтыми, оранжевыми, то есть яркими, говорит он, остальные линии имеют второстепенное значение и не должны отвлекать водителя от движения.
Вопрос появления новой разметки на дорогах, в частности в Москве, пока не решен, отмечает господин Мухортиков. Распоряжением правительства РФ №2438-р от 4 ноября 2017 года утвержден перечень стандартов, обязательных к соблюдению. «Он в текущей редакции ссылается на старый ГОСТ 2011 года, аналогичная ссылка есть и в ПДД,— пояснил Андрей Мухортиков.
Даже оперативное внесение изменений в документы не гарантирует, что в 2018 году в столице появится новая разметка. Такие решения, говорят в ЦОДД, принимаются не быстро: сначала готовится проект организации движения, затем его утверждает департамент транспорта Москвы, после чего документ направляется в департамент ЖКХ, а откуда уже попадает к исполнителю — ГБУ «Автомобильные дороги», которое наносит новую разметку при плановой замене асфальта. «Проекты готовятся заранее, до начала ремонтного сезона, в связи с ГОСТом в них надо будет снова вносить коррективы, это долгая,— говорит господин Мухортиков.— В любом случае, даже если стандарт станет обязательным, я не вижу оснований, что в Москве надо будет что-то срочно менять: все применяющиеся сегодня варианты по-прежнему допускаются».
Иван Буранов
В России введен предварительный национальный стандарт, куда вошли новые виды дорожных знаков, включая «Выделенная трамвайная полоса», «Запрет въезда на перекресток в случае затора», «Глухие пешеходы» и «Уступи всем, и можно направо». Часть указателей уже применяются в столице в экспериментальном режиме, теперь они закреплены официальным документом.
Часть указателей уже применяются в столице в экспериментальном режиме, теперь они закреплены официальным документом.
Читать далее
По обращениям граждан «двойная сплошная» разметка на некоторых дорогах в Пскове будет скорректирована
Заседание городской комиссии по обеспечению безопасности дорожного движения состоялось в Пскове в понедельник, 22 июня. В ее работе приняли участие представители городской власти, ГИБДД по городу Пскову, общественности и председатель Комитета по транспорту и дорожному хозяйству Псковской области Борис Елкин.
Одним из главных вопросов повестки дня стала целесообразность корректировки схемы организации дорожного движения в части нанесения сплошной линии разметки на отдельных участках улично-дорожной сети города Пскова. Речь идет о новой двойной сплошной разметке на улицах Вокзальной, Маргелова, 128-й Стрелковой дивизии, Советской Армии, Рокоссовского и Коммунальной, которая запретила левые повороты при заезде и выезде с прилегающих территорий. В связи с этим в органы власти стали поступать многочисленные обращения граждан.
Речь идет о новой двойной сплошной разметке на улицах Вокзальной, Маргелова, 128-й Стрелковой дивизии, Советской Армии, Рокоссовского и Коммунальной, которая запретила левые повороты при заезде и выезде с прилегающих территорий. В связи с этим в органы власти стали поступать многочисленные обращения граждан.
Начальник ГИБДД УМВД России по городу Пскову Владимир Папорт пояснил, что «двойная сплошная» обусловлена рекомендациями по безопасности дорожного движения, когда исключаются левые повороты на дорогах с 4-полосным движением. Однако на большинстве указанных объектов ГИБДД не возражает против нанесения разметки 1.11 «Сплошная и прерывистая линия», что позволит поворачивать налево во дворы, но при этом разрешит выезжать из дворов только направо.
По поручению председателя Комиссии, Главы Администрации города Пскова Александра Братчикова, в ближайшее время будут внесены изменения в разметку и установлены соответствующие дорожные знаки.
В продолжение заседания были также рассмотрены вопросы, предложенные Администрацией Псковской области. Так, комиссия решила организовать дополнительный пешеходный переход на улице Звездной в районе дома №11. Также будет проработан вопрос об обустройстве светофора на перекрестке улиц Шестака и Доставалова. Еще один пешеходный переход появится на улице Алмазной.
Так, комиссия решила организовать дополнительный пешеходный переход на улице Звездной в районе дома №11. Также будет проработан вопрос об обустройстве светофора на перекрестке улиц Шестака и Доставалова. Еще один пешеходный переход появится на улице Алмазной.
Фотографии пресс-службы Администрации Псковской области
В России утвержден новый стандарт дорожной разметки
Новый ГОСТ дорожной разметки, утвержденный Росстандартом, содержит ряд нововведений, которые вскоре станут заметны всем участникам движения. Документ, который готовился по заказу Росавтодора, вступает в силу 1 июня 2018 года, сообщает газета «Коммерсант».
Согласно стандарту, все основные виды дорожной разметки, разделяющей потоки и полосы движения (одинарная и двойная сплошная, прерывистая, комбинация прерывистой и сплошной) могут быть как белого, так и желтого цвета. До сих пор желтая маркировка применялась только для обозначения зон запрета стоянки. Синими могут стать прерывистые линии, используемые для направления движения на перекрестках.
Вводится ряд новых обозначений, которые наносятся на асфальт: знак, обозначающий станцию зарядки электромобилей, разметка типа «вафельница» (зона, в которую запрещено въезжать во время затора на перекрестке). Последняя в качестве эксперимента, отметим, уже применяется на 30 перекрестках в Москве, новым ГОСТом она будет легализована. Стандартом впервые предусмотрена стрелка, обозначающая зону разворота,– в старом ГОСТе ее не было, были только стрелки поворотные.
Как рассказал разработчик стандарта гендиректор центра инженерно-технических исследований (ЦИТИ) «Дорконтроль» Владимир Свежинский, разметка желтого цвета, пояснил он, позволяет «улучшить ее видимость», особенно в регионах, где обильно выпадает снег. Синяя разметка будет применяться для обозначения платной и бесплатной парковки, но конкретные правила применения закрепит в новой редакции другого ГОСТа, который сейчас также перерабатывается. Любопытно, что разметка 1.7 (синяя по новому ГОСТу) могла использоваться в качестве разметки парковочных зон до июля 2017 года: в ПДД были внесены изменения, и эту опцию убрали.
Замначальника ситуационного центра московского ЦОДД Андрей Мухортиков нововведения поддержал, отметив важность разметки, обозначающий разворот. «До сих пор под знаком «Разворот» размещалась стрелка с поворотом, что, конечно, путало водителей,– рассказал он.– Логика появления синих линий понятна, она уже давно применяется в Европе для обозначения парковочных зон». Cплошные осевые линии, обозначения обочин, влияющие на безопасность, должны быть белыми, желтыми, оранжевыми, то есть яркими, говорит он, остальные линии имеют второстепенное значение и не должны отвлекать водителя от движения.
Разворот через двойную сплошную \ Акты, образцы, формы, договоры \ Консультант Плюс
]]>Подборка наиболее важных документов по запросу Разворот через двойную сплошную (нормативно–правовые акты, формы, статьи, консультации экспертов и многое другое).
Статьи, комментарии, ответы на вопросы: Разворот через двойную сплошную Открыть документ в вашей системе КонсультантПлюс:Статья: О причинной связи в преступлениях, предусмотренных ст.
 264 УК РФ
264 УК РФ(Хромов Е.В., Зябликов А.Ю.)
(«Актуальные проблемы российского права», 2021, N 4)Д. выехал на перекресток на запрещающий сигнал светофора (нарушение п. 1.3, 1.5, 6.2, 8.1, 9.1, 9.7, 10.1 ПДД РФ). С противоположной стороны перекрестка водитель А., находящийся в крайнем левом ряду, предназначенном для поворота налево, приступил к выполнению маневра разворота вне перекрестка через двойную сплошную линию разметки, полагая, что встречному транспорту движение прямо запрещено, и не уступил дорогу двигавшемуся во встречном направлении автомобилю под управлением Д. (нарушение п. 1.3, 1.5, 8.1, 8.8, 9.1, 9.2, 9.7, 10.1 ПДД РФ). В результате ДТП пассажиру автомобиля А. причинены телесные повреждения, относящиеся к категории тяжких. Согласно выводам автотехнической экспертизы, водитель Д. располагал технической возможностью избежать столкновения в момент появления автомашины под управлением А. в полосе его движения .Нормативные акты: Разворот через двойную сплошную
Решение Верховного Суда РФ от 17.
 01.2012 N ГКПИ11-1938
01.2012 N ГКПИ11-1938Утверждение заявителя о том, что на дорогах с двусторонним движением, имеющих три полосы, обозначенные разметкой (за исключением разметки 1.9), средняя полоса не может использоваться для движения в обоих направлениях, ошибочно. Пример разметки таких дорог с использованием средней полосы для движения в обоих направлениях приведен в диаграмме A-3, ссылка на которую содержится в пункте 9 приложения к Протоколу о разметке дорог к Европейскому соглашению, дополняющему Конвенцию о дорожных знаках и сигналах, открытую для подписания в Вене 8 ноября 1968 г. (Женева, 1 марта 1973 г.). В названном пункте указано, что на дорогах с двусторонним движением, имеющих три полосы движения, полосы следовало бы, как правило, указывать прерывистыми линиями (диаграмма A-3). Одна или две сплошные линии или одна прерывистая линия, проведенные рядом со сплошной линией, должны применяться лишь в особых случаях. Указанный Протокол вступил в силу для СССР, правопреемником которого является Российская Федерация, 25 апреля 1985 г.

%PDF-1.4 % 1 0 объект > эндообъект 6 0 объект /Заголовок /Предмет /Автор /Режиссер /Ключевые слова /CreationDate (D:20220105120124-00’00’) /ModDate (D:201
 $]=Q-#Hy:R,s.>/ӧd>eHxk_q’]?_~~|yCqyTM$PLtz
Z,Cm*k=KFZo»2(A14}3HA\$,f7Y3S,j]AXusV1BA ܆U+Fx
$]=Q-#Hy:R,s.>/ӧd>eHxk_q’]?_~~|yCqyTM$PLtz
Z,Cm*k=KFZo»2(A14}3HA\$,f7Y3S,j]AXusV1BA ܆U+FxНепрерывный и прерывистый динамический кроссовер в Переохлажденная вода в компьютерном моделировании
Реферат
динамическое кроссоверное поведение переохлажденной воды, как описано
методом WAIL на основе первого принципа был исследован потенциал WAIL. Ниже
вторая критическая точка жидкость-жидкость, вязкость показывает
прерывистый скачок, соответствующий фазовому переходу первого рода
между жидкостью высокой плотности и жидкостью низкой плотности.Выше
критической точки непрерывный переход происходит только с первым
производная вязкости разрывна, а динамический кроссовер
температура примерно на 8 К ниже температуры термодинамического переключения.
Сдвиг на 8К можно объяснить задержкой динамического кроссовера, который
не происходит до тех пор, пока более вязкая жидкость не начнет преобладать в
населения и блокирует поток. На основе эффектов конечных размеров
наблюдается в наших симуляциях, мы считаем, что динамическая неоднородность
может наблюдаться выше критической точки в закрытой воде, когда
ограничение находится на шкале длины короче, чем пространственная корреляция.
Несмотря на вездесущность и важность воды, свойства глубоко охлажденной воды ниже однородной Температура зародышеобразования около 237 К до сих пор является предметом споров. 1−13 При температуре стеклования 136 К вода является самой сильной жидкость когда-либо идентифицирована. 14−16 Наоборот, над однородным температура зародышеобразования, вода является очень хрупкой жидкостью. 14 Где-то между температурой стеклования и однородной температуры зародышеобразования, должно быть пересечение между сильной и хрупкой динамикой. 17 точная природа такого динамичного кроссовера была неуловимой и противоречивой.
Экспериментальное исследование динамического кроссовера обычно
сделано в заключении, 18−21 или с другим раствором для подавления замерзания. 22,23 Теоретическое моделирование с моделями Jagla, 24 ST2, 25 SPC/E, 26,27 и TIP4P 28 показало перекрестное поведение,
хотя насколько реалистично эти модели отражают физику истинной воды
— открытый вопрос. 4,12 Большинство используемых водных моделей
для моделирования были созданы путем подгонки к экспериментальным свойствам.
Недавно была выпущена водная модель WAIL, 29 .
разработан путем подгонки к расчетам электронной структуры 30,31 , выполненным для качества связанных кластеров. 32 Модель WAIL предсказывает, что температура плавления ( T M ) воды составит ∼270 K, а температура максимума
плотность (TMD) около 9 ° C, что хорошо согласуется с экспериментальными
ценности.Моделирование с потенциалом WAIL менее восприимчиво к
предубеждения, которые могли быть введены, когда модель соответствовала экспериментальным
наблюдаемые. Симуляции с WAIL отражают предсказание от
лежащий в основе метод первого принципа, используемый для параметризации, 33 при ограничении простых выражений энергии
используется для потенциала.
4,12 Большинство используемых водных моделей
для моделирования были созданы путем подгонки к экспериментальным свойствам.
Недавно была выпущена водная модель WAIL, 29 .
разработан путем подгонки к расчетам электронной структуры 30,31 , выполненным для качества связанных кластеров. 32 Модель WAIL предсказывает, что температура плавления ( T M ) воды составит ∼270 K, а температура максимума
плотность (TMD) около 9 ° C, что хорошо согласуется с экспериментальными
ценности.Моделирование с потенциалом WAIL менее восприимчиво к
предубеждения, которые могли быть введены, когда модель соответствовала экспериментальным
наблюдаемые. Симуляции с WAIL отражают предсказание от
лежащий в основе метод первого принципа, используемый для параметризации, 33 при ограничении простых выражений энергии
используется для потенциала.
Было показано, что потенциал WAIL
поддерживает две формы
жидкая вода в переохлажденном режиме с различной плотностью. 15 Две формы, 34 высокая
жидкости высокой плотности (HDL) и жидкости низкой плотности (LDL), имеют критическое
температура около 207 К при 50 МПа.Выше критической точки,
две микроскопические формы сосуществуют в одной фазе по линии Видома; 35,36 ниже критической точки, резкий переход между двумя формами
наблюдается в соответствии с фазовым переходом первого рода в нашей
моделирование.
15 Две формы, 34 высокая
жидкости высокой плотности (HDL) и жидкости низкой плотности (LDL), имеют критическое
температура около 207 К при 50 МПа.Выше критической точки,
две микроскопические формы сосуществуют в одной фазе по линии Видома; 35,36 ниже критической точки, резкий переход между двумя формами
наблюдается в соответствии с фазовым переходом первого рода в нашей
моделирование.
Кинетика структурной релаксации воды WAIL
Не было
изучал. В то время как большинство существующих симуляций динамического кроссовера в переохлажденных
воды сосредоточились на константе диффузии, подогнав к степени
закон масштабирования, предсказанный теорией связи мод, вязкость 37 является одним из наиболее прямых экспериментальных наблюдаемых
для определения хрупкости. 38 Вычислительный
изучение вязкости переохлажденной воды в литературе встречается редко.
В данной работе мы измеряли вязкость воды с помощью неравновесного
молекулярной динамики (NEMD) путем приложения внешней силы с синусоидальной
профиль. 39 Часто упоминаемый подход
как метод косинусного ускорения. 40 Гесс сравнил четыре различных подхода к расчету вязкости
воды и нашел, что метод косинусного ускорения является наиболее надежным. 40 По сравнению с подходом, основанным на Грине-Кубо,
подход NEMD обычно сходится быстрее.Это важно для
моделирование переохлажденной воды из-за необходимости длинных траекторий
при низких температурах.
39 Часто упоминаемый подход
как метод косинусного ускорения. 40 Гесс сравнил четыре различных подхода к расчету вязкости
воды и нашел, что метод косинусного ускорения является наиболее надежным. 40 По сравнению с подходом, основанным на Грине-Кубо,
подход NEMD обычно сходится быстрее.Это важно для
моделирование переохлажденной воды из-за необходимости длинных траекторий
при низких температурах.
Если не указано иное, измерения вязкости
были выполнены
в орторомбическом ящике со средним размером 2,2 нм ×
2,2 нм × 4,4 нм, содержащий 686 молекул воды. Коробка была построена
из начальных конфигураций, выбранных ранее Li et al. 15 и воспроизведены в измерении Z .
Более длинный размер Z требуется для обеспечения
справедливость уравнения Навье–Стокса. 40 Новый бокс уравновешивался в течение 7 нс. Косинусное ускорение
применяли после уравновешивания в течение 20 нс со скоростью
профиль, измеренный за последние 15 нс. Требуется такое длинное измерение
из-за медленной динамики переохлажденных температур. Для выбранных
точки температуры и давления, описанные позже, большая симуляция
ящик, содержащий 2744 молекулы воды, использовался для оценки конечного
эффект размера. Большая коробка имеет приблизительный размер 4,4 нм.
× 4,4 нм × 4.4 нм. Всего 3200 измерений вязкости
были выполнены, чтобы уменьшить планку погрешности измеренных вязкостей.
Это соответствует примерно 70 мкс траектории.
Требуется такое длинное измерение
из-за медленной динамики переохлажденных температур. Для выбранных
точки температуры и давления, описанные позже, большая симуляция
ящик, содержащий 2744 молекулы воды, использовался для оценки конечного
эффект размера. Большая коробка имеет приблизительный размер 4,4 нм.
× 4,4 нм × 4.4 нм. Всего 3200 измерений вязкости
были выполнены, чтобы уменьшить планку погрешности измеренных вязкостей.
Это соответствует примерно 70 мкс траектории.
Метод суммирования Эвальда применялся для лечения дальнодействующей электростатики.
Уравнение движения интегрировалось с шагом по времени 0,5
fs с водородом, предполагающим массу изотопа дейтерия. То
Выполнены подгонка Фогеля-Фулхера-Таммана (VFT) и подгонка по Аррениусу.
путем минимизации взвешенной суммы квадратов остатков (WSSR), где
вклад каждой точки взвешивался обратным значением
квадрат ошибки.Планки погрешностей были определены путем повторной выборки начальной загрузки
измеряемой вязкости. Ресемплинг производился с заменами.
а показывает вязкость как функция температуры для давлений от 0,1 до 70 МПа. Четкий переход от сильного к хрупкому наблюдается при низкотемпературная вязкость, показывающая зависимость Аррениуса и высокотемпературная вязкость, показывающая кинетику VFT. 41 Вода WAIL имеет переход жидкость–жидкость первого рода свыше 50 МПа. При 70 МПа происходит переход жидкость–жидкость ниже 200 К, что является самой низкой температурой, исследованной в этом Работа.Таким образом, при этом давлении можно наблюдать только кинетику VFT ЛПВП.
(а) Вязкость
переохлажденной воды в зависимости от температуры
на давление от 0,1 до 70 МПа. Термодинамический переход ЛПНП-ЛПВП
температуры ( T therm ) показаны черным цветом
точки. (б) Вязкость переохлажденной воды при 50 МПа показывает разрыв
между двумя жидкими формами. Вязкость метастабильных ЛПВП
при 205 К обозначается как H, а вязкость метастабильного ЛПНП
при 210 К обозначается как L.(в) Вязкость переохлажденной воды при 30
и 40 МПа. Синие точки были рассчитаны с помощью окна моделирования, которое
в 4 раза больше. (г) Вязкость переохлажденной воды при 0,1, 10,
и 20 МПа показывает непрерывный переход между формами ЛПНП и ЛПВП.
На верхних панелях планки погрешностей видны сквозь полые символы.
Во многих случаях планка погрешности практически равна нулю на графике логарифмической шкалы.
и может рассматриваться как одна горизонтальная линия в центре.
Синие точки были рассчитаны с помощью окна моделирования, которое
в 4 раза больше. (г) Вязкость переохлажденной воды при 0,1, 10,
и 20 МПа показывает непрерывный переход между формами ЛПНП и ЛПВП.
На верхних панелях планки погрешностей видны сквозь полые символы.
Во многих случаях планка погрешности практически равна нулю на графике логарифмической шкалы.
и может рассматриваться как одна горизонтальная линия в центре.
Вязкость при 50 МПа выделена в b. При этом давлении,
вода WAIL подвергается
фазовый переход первого рода при ~207 К. 15 HDL показывает точное соответствие хрупкой кинетике выше
температура перехода, а вязкость ЛПНП соответствовала Аррениусу
кинетика ниже температуры перехода. Вязкость показывает прерывистую
скачком при ∼207 K. Хотя первая производная динамического
переменная, такая как вязкость, как ожидается, будет прерывистой
переход от сильного к хрупкому, большинство существующих исследований предполагают непрерывный
изменение самой динамической переменной при подгонке через переход
линия. Наше моделирование показывает, что во время фазового перехода первого рода
между двумя жидкостями разрыв в самой динамической переменной
следует ожидать.Это неудивительно, учитывая, что две жидкости
имеют разную вязкость. Подобный разрыв в константе диффузии
было показано в предыдущих исследованиях с использованием модели Jagla. 24
Наше моделирование показывает, что во время фазового перехода первого рода
между двумя жидкостями разрыв в самой динамической переменной
следует ожидать.Это неудивительно, учитывая, что две жидкости
имеют разную вязкость. Подобный разрыв в константе диффузии
было показано в предыдущих исследованиях с использованием модели Jagla. 24
Чтобы подтвердить это наблюдение, мы вычислили
вязкость метастабильных
жидкости через линию перехода. В переохлажденной воде, хотя
лед термодинамически более стабилен, он недоступен в нашем
шкала времени моделирования. При 210 К и 50 МПа, хотя фаза ЛПВП
более стабилен, ЛПНП могут существовать сотни наносекунд, прежде чем трансформироваться
спонтанно и необратимо на ЛПВП. 15 В б, р
вязкость метастабильной фазы ЛПНП перед спонтанным переходом
обозначен как L. Точно так же вязкость метастабильной фазы ЛПВП
при 205 K отмечен как H. Метастабильные точки остаются близкими к экстраполированным
кривые вязкости, полученные путем подгонки к более стабильным вязкостям жидкости,
отчетливо видна кинетическая неоднородность поперек жидкости-жидкости
линия перехода. Это подтверждает, что скачок вязкости
наблюдаемое не является артефактом нашей процедуры подгонки.
Это подтверждает, что скачок вязкости
наблюдаемое не является артефактом нашей процедуры подгонки.
Вязкость показана переохлажденная вода WAIL при 30 и 40 МПа. в с. На этих давления, ЛПНП и ЛПВП больше не являются двумя отдельными фазами. Для макроскопического системы, можно было бы ожидать, что вязкость будет непрерывной, поскольку два жидкие формы колеблются в однофазном режиме. Однако c ясно показывает разрыв по вязкости по линии Видома.
Вблизи критической точки, структурные колебания коррелируют на большом расстоянии, которое больше или сравнимо с размер нашей коробки моделирования.Временной след плотности коробки, как показано в , указывает что система сильно колеблется между конформациями ЛПВП и ЛПНП, при этом вся коробка представляет собой ЛПВП или ЛПНП, а не смесь. Для макроскопическая система, только домены системы, а не все примет формы ЛПВП или ЛПНП, и, таким образом, измеренная вязкость не отражают истинной вязкости макроскопической системы.
Трассировка времени
плотности коробки при 30 МПа 210 К (вверху) и 40 МПа
210 К (внизу). Горизонтальные линии — ожидаемая плотность для
ЛПВП и ЛПНП соответственно.
Горизонтальные линии — ожидаемая плотность для
ЛПВП и ЛПНП соответственно.
Чтобы оценить, действительно ли эффект конечного размера объясняет очевидный разрыва вязкости, мы повторили расчеты вязкости для выбранных точек с помощью ящика, содержащего 2744 молекулы воды, что в 4 раза больше, чем другие ящики. Синие точки в c обозначают вязкость рассчитывается с большей коробкой. Близко к критической точке на 210 K, большая коробка привела к гораздо большей вязкости, с непрерывным кроссовером чуть выше 205 K.
Хотя вязкость, измеренная с помощью большего ящика, значительно больше при 210 К, разница уменьшается с изменением температуры дальше от критической температуры, что соответствует ожиданиям что более короткие длины пространственной корреляции дальше от критического точка минимизирует эффект конечного размера.
д показывает
вязкость в зависимости от температуры для 0,1, 10 и 20 МПа.
Вязкость демонстрирует непрерывный переход от хрупкого к сильному.
по мере снижения температуры. Только первая производная вязкости
прерывистый. При этих давлениях корреляционная длина достаточно
короткий из-за большего расстояния от критической точки. Даже для
температуры и давления, близких к линии Видома, только области
ЛПНП и ЛПВП существуют в 686 симуляции воды.
Только первая производная вязкости
прерывистый. При этих давлениях корреляционная длина достаточно
короткий из-за большего расстояния от критической точки. Даже для
температуры и давления, близких к линии Видома, только области
ЛПНП и ЛПВП существуют в 686 симуляции воды.
Температура для динамического кроссовера на 0.1, 10 и 20 МПа может определяется точкой, в которой вязкость VFT равна вязкость по Аррениусу. Динамическая переходная температура при давлениях выше 20 МПа оценивается линейной экстраполяцией поведение давления, потому что прямое измерение температуры кроссовера при этих давлениях является сложной задачей из-за эффектов конечного размера. То линия динамического кроссовера обрывается при критической температуре 207 К. Ниже этой температуры наблюдается прерывистая кинетика через линию фазового перехода.
В
линия динамического кроссовера построена вместе с термодинамическим переходом
линия. Линия термодинамического перехода следует границе раздела фаз
ниже критической точки. Выше критической точки фаза отсутствует.
переход, популяция переключается с преобладания ЛПНП на ЛПВП
доминируют над линией Видома. Таким образом, термодинамический «переход»
линия на рисунке следует за линией Видома, которая аппроксимируется с помощью
точки перегиба изобар плотности и максимумы изотермосжимаемости
опубликовано ранее. 15 Из видно, что динамический
кроссовер происходит при более низкой температуре, чем термодинамическое переключение
выше критической точки. Эта разница также очевидна в А.
Выше критической точки фаза отсутствует.
переход, популяция переключается с преобладания ЛПНП на ЛПВП
доминируют над линией Видома. Таким образом, термодинамический «переход»
линия на рисунке следует за линией Видома, которая аппроксимируется с помощью
точки перегиба изобар плотности и максимумы изотермосжимаемости
опубликовано ранее. 15 Из видно, что динамический
кроссовер происходит при более низкой температуре, чем термодинамическое переключение
выше критической точки. Эта разница также очевидна в А.
Линия динамического кроссовера и линия термодинамического перехода. То линия термодинамического перехода следует за линией фазового перехода (сплошная) ниже критической температуры, а линия Видома выше критической. температура (пунктир). Линия динамического кроссовера заканчивается в критической точке. точка. Ниже критической точки вязкость становится прерывистой. при пересечении фазовой границы.
Было показано, что вдали от критической точки
место
максимума для различных функций отклика, таких как теплоемкость
и изотермосжимаемость, не обязательно согласны.![]() 42 В этой работе мы будем предполагать, что линия Widom 35 близка к линии 50–50, где каждый
из двух микроскопических форм жидкостей имеет мольную долю около 50%.
Сдвиг между динамическим кроссовером и термодинамическим переключением
можно понять, рассматривая смесь льда и воды с малым
кристаллы льда, растворенные в воде.Механическое измерение вязкости
такой смеси, 43 , с использованием таких методов, как
как метод капиллярного потока 43 или
вискозиметр с падающей сферой, 44 не покажет
вязкость льда, потому что лед течет внутри более текучей жидкости
при измерении вязкости. Динамический кроссовер не произойдет, пока
образовалось достаточное количество льда, чтобы лед больше не текла
без вдавливания друг в друга, что интуитивно должно происходить
когда мольная доля льда значительно превышает 50%.
42 В этой работе мы будем предполагать, что линия Widom 35 близка к линии 50–50, где каждый
из двух микроскопических форм жидкостей имеет мольную долю около 50%.
Сдвиг между динамическим кроссовером и термодинамическим переключением
можно понять, рассматривая смесь льда и воды с малым
кристаллы льда, растворенные в воде.Механическое измерение вязкости
такой смеси, 43 , с использованием таких методов, как
как метод капиллярного потока 43 или
вискозиметр с падающей сферой, 44 не покажет
вязкость льда, потому что лед течет внутри более текучей жидкости
при измерении вязкости. Динамический кроссовер не произойдет, пока
образовалось достаточное количество льда, чтобы лед больше не текла
без вдавливания друг в друга, что интуитивно должно происходить
когда мольная доля льда значительно превышает 50%.
Мы
предположить, что в переохлажденной воде выше критической температуры
две микроскопические формы жидкости быстро колеблются, и вязкость
жидкости преобладает форма с меньшей вязкостью, которая
является ЛПВП. Выше критической точки динамика VFT при более высокой температуре
вызвано увеличением популяции доменов ЛПНП и перекрестным
к режиму Аррениуса обусловлено образованием достаточного количества
ЛПНП, чтобы заглушить систему. Это объяснит наблюдение, что
кинетическая температура перехода происходит ниже термодинамической, Widom,
температура переключения.Ранее было показано, что помехи
ожидается, что гранулированные частицы будут следовать кинетике VTF. 45
Выше критической точки динамика VFT при более высокой температуре
вызвано увеличением популяции доменов ЛПНП и перекрестным
к режиму Аррениуса обусловлено образованием достаточного количества
ЛПНП, чтобы заглушить систему. Это объяснит наблюдение, что
кинетическая температура перехода происходит ниже термодинамической, Widom,
температура переключения.Ранее было показано, что помехи
ожидается, что гранулированные частицы будут следовать кинетике VTF. 45
Стоит отметить, что наше наблюдение
смены
линия динамического перехода к более низкой температуре из линии Widom
также наблюдается экспериментально. 46 Например, рисунок 1 ссылки (46) Чена и др. ясно показывает динамическое пересечение в
α-релаксация должна быть при более низкой температуре, чем максимальная в
дифференциальной сканирующей калориметрии, хотя Чен пришел к выводу, что два
температуры согласуются в пределах экспериментальных погрешностей.Если наше объяснение
сдвиг действительно верен, мы ожидаем аналогичные сдвиги между
две линии появляются в некоторых других жидкостях.
Отмечаем HDL форма сама по себе также показывает динамику VFT, потому что жидкость HDL ниже критической температуры показывает хрупкую кинетику. Это согласуется с наблюдением кинетики VFT других стекол. формирователи. Без образования ЛПНП в фазе ЛПВП вязкость ЛПВП остается относительно низким, и наблюдается неоднородность по всему линия фазового перехода.
Отметим, что разрыв в
вязкость с моделью WAIL
не доказывает фазовый переход жидкость-жидкость первого рода
в настоящей воде. Однако модель WAIL создавалась на базе только электронных
структурировать информацию в качестве входных данных и, таким образом, основывается на первом принципе
модель. В воде WAIL вязкость смеси ЛПНП и ЛПВП составляет
в одной фазе преобладает вязкость менее вязких ЛПВП
форма. Динамический кроссовер происходит только тогда, когда начинается популяция ЛПНП.
доминировать над жидкостью.Хотя этот аргумент объясняет сдвиг
в динамическом кроссовере по вязкости от термодинамического переключения
линии, нам не сразу ясно, будет ли подобный вывод
можно нарисовать, когда константа диффузии используется для характеристики динамики
потому что уравнение Стокса-Эйнштейна может не выполняться при пересечении
на линию Видома. Справедливость заключения при других динамических
переменные используются для характеристики динамического кроссовера, требует дальнейшего
изучение.
Справедливость заключения при других динамических
переменные используются для характеристики динамического кроссовера, требует дальнейшего
изучение.
Вблизи критической точки, конечный размер эффект моделирования приводит к отклонению от кинетики VFT; это приводит к разрыву кажущейся вязкости по линии Видома.Такой разрыв температура выше критической не должна существовать в макроскопических образцах но может наблюдаться экспериментально в закрытых системах. Ниже критическая точка, вязкость в нашем моделировании показывает явный разрыв, которое можно объяснить только переходом первого рода между двумя разные фазы. Многие существующие исследования перехода от хрупкого к сильному в переохлажденной воде и других стеклообразователях подходят VFT и Кинетика Аррениуса с разрывной первой производной, но непрерывной вязкость.Наша работа показывает, что сама вязкость может быть прерывистой. когда основной переход действительно первого порядка.
Произошла ошибка при настройке пользовательского файла cookie
Этот сайт использует файлы cookie для повышения производительности. Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.
Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.
Настройка браузера на прием файлов cookie
Существует множество причин, по которым файл cookie не может быть установлен правильно. Ниже приведены наиболее распространенные причины:
- В вашем браузере отключены файлы cookie.Вам необходимо сбросить настройки браузера, чтобы принять файлы cookie, или спросить вас, хотите ли вы принимать файлы cookie.
- Ваш браузер спрашивает, хотите ли вы принимать файлы cookie, и вы отказались. Чтобы принять файлы cookie с этого сайта, нажмите кнопку «Назад» и примите файл cookie.
- Ваш браузер не поддерживает файлы cookie. Попробуйте другой браузер, если вы подозреваете это.
- Дата на вашем компьютере в прошлом. Если часы вашего компьютера показывают дату до 1 января 1970 г.,
браузер автоматически забудет файл cookie.Чтобы это исправить, установите правильное время и дату на своем компьютере.

- Вы установили приложение, которое отслеживает или блокирует установку файлов cookie. Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.
Почему этому сайту требуются файлы cookie?
Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу. Предоставить доступ без файлов cookie потребует от сайта создания нового сеанса для каждой посещаемой вами страницы, что замедляет работу системы до неприемлемого уровня.
Что сохраняется в файле cookie?
Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в файле cookie; никакая другая информация не фиксируется.
Как правило, в файле cookie может храниться только та информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта. Например, сайт
не может определить ваше имя электронной почты, если вы не решите ввести его. Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступ к
остальной части вашего компьютера, и только сайт, создавший файл cookie, может его прочитать.
Например, сайт
не может определить ваше имя электронной почты, если вы не решите ввести его. Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступ к
остальной части вашего компьютера, и только сайт, создавший файл cookie, может его прочитать.
произвольных высокого порядка Разрывной метод Галеркина для упругих волн на неструктурированных сетках — V. Шаг по локальному времени и p-адаптивность | Международный геофизический журнал
Резюме
В этой статье описывается расширение произвольного метода разрывного Галеркина высокого порядка (ADER-DG) для обработки локально меняющегося полиномиального спуска базисных функций, так называемой p -адаптивности, а также локально изменяющихся временных шагов, которые могут быть отличается от одного элемента к другому.Адаптивная версия схемы p полезна в сложных трехмерных моделях с мелкомасштабными элементами, которые должны быть объединены в сетку с достаточно мелкими элементами для захвата необходимых геометрических деталей, представляющих интерес. Использование постоянной высокой полиномиальной степени базисных функций во всей вычислительной области может привести к неоправданно высокой нагрузке ЦП, поскольку хорошее пространственное разрешение на поверхности уже может быть получено мелкой сеткой. Следовательно, в некоторых случаях может быть более адекватным использовать метод более низкого порядка для небольших элементов, чтобы уменьшить нагрузку на ЦП без значительной потери точности.Для дальнейшего повышения вычислительной эффективности мы представляем новый алгоритм локального шага по времени (LTS). Для обычных явных схем шага по времени элемент с наименьшим шагом по времени, вытекающий из критерия устойчивости метода, будет диктовать свой шаг по времени всем остальным элементам расчетной области. Напротив, при использовании шага по локальному времени каждый элемент может использовать свой оптимальный шаг по времени, заданный условием локальной устойчивости. Предлагаемый нами алгоритм LTS для ADER-DG является очень общим и не требует временной синхронизации между элементами.
Использование постоянной высокой полиномиальной степени базисных функций во всей вычислительной области может привести к неоправданно высокой нагрузке ЦП, поскольку хорошее пространственное разрешение на поверхности уже может быть получено мелкой сеткой. Следовательно, в некоторых случаях может быть более адекватным использовать метод более низкого порядка для небольших элементов, чтобы уменьшить нагрузку на ЦП без значительной потери точности.Для дальнейшего повышения вычислительной эффективности мы представляем новый алгоритм локального шага по времени (LTS). Для обычных явных схем шага по времени элемент с наименьшим шагом по времени, вытекающий из критерия устойчивости метода, будет диктовать свой шаг по времени всем остальным элементам расчетной области. Напротив, при использовании шага по локальному времени каждый элемент может использовать свой оптимальный шаг по времени, заданный условием локальной устойчивости. Предлагаемый нами алгоритм LTS для ADER-DG является очень общим и не требует временной синхронизации между элементами. Благодаря подходу ADER на интерфейсах элементов автоматически обеспечивается точная временная интерполяция, так что вычислительные затраты очень малы и метод поддерживает одинаковый высокий порядок точности в пространстве и времени, как в обычных схемах ADER-DG с глобально постоянный шаг по времени. Однако метод LTS ADER-DG в вычислительном отношении намного более эффективен для задач с сильно различающимися размерами элементов или параметрами материалов, поскольку он позволяет значительно сократить общее количество обновлений элементов.Это особенно справедливо для неструктурированных тетраэдрических сеток, содержащих сильно вырожденные элементы, так называемые щепки. Мы показываем результаты численной сходимости и время ЦП для схем LTS ADER-DG до шестого порядка по пространству и времени на неправильных тетраэдрических сетках, содержащих элементы самого разного размера, а также на тетраэдрических сетках, содержащих осколки. Дальнейшая проверка алгоритма обеспечивается результатами, полученными для эталонной задачи слоя над полупространством (LOH.
Благодаря подходу ADER на интерфейсах элементов автоматически обеспечивается точная временная интерполяция, так что вычислительные затраты очень малы и метод поддерживает одинаковый высокий порядок точности в пространстве и времени, как в обычных схемах ADER-DG с глобально постоянный шаг по времени. Однако метод LTS ADER-DG в вычислительном отношении намного более эффективен для задач с сильно различающимися размерами элементов или параметрами материалов, поскольку он позволяет значительно сократить общее количество обновлений элементов.Это особенно справедливо для неструктурированных тетраэдрических сеток, содержащих сильно вырожденные элементы, так называемые щепки. Мы показываем результаты численной сходимости и время ЦП для схем LTS ADER-DG до шестого порядка по пространству и времени на неправильных тетраэдрических сетках, содержащих элементы самого разного размера, а также на тетраэдрических сетках, содержащих осколки. Дальнейшая проверка алгоритма обеспечивается результатами, полученными для эталонной задачи слоя над полупространством (LOH. 1), предложенной Тихоокеанским центром инженерных исследований землетрясений.Наконец, мы представляем реалистичное приложение для моделирования землетрясений и предсказания движения грунта для альпийской долины Гренобля.
1), предложенной Тихоокеанским центром инженерных исследований землетрясений.Наконец, мы представляем реалистичное приложение для моделирования землетрясений и предсказания движения грунта для альпийской долины Гренобля.
1 Введение
Крупномасштабные приложения в численной сейсмологии, включая реалистичные свойства материалов и сложную геометрию, обычно по-прежнему требуют огромных усилий при построении моделей, создании сетки, хранении данных на компьютере и процессорном времени. В прошлом достижения в области создания сеток привели к автоматизированным алгоритмам, которые создают неструктурированные тетраэдрические сетки даже для очень сложных геометрических форм.Однако расчетная область может иметь зоны, в которых неизбежны очень мелкие элементы сетки, чтобы разрешить интересующие геометрические особенности, например, осадочные бассейны, складчатые и разломные резервуары или топографию поверхности. Кроме того, в других частях расчетной области могут быть допустимы достаточно крупные элементы.
Кроме того, в других частях расчетной области могут быть допустимы достаточно крупные элементы.
В целом явные методы высокого порядка сталкиваются с двумя основными недостатками для таких сильно неоднородных сеток, в частности, если сетка содержит в основном крупные элементы и лишь несколько очень мелких элементов в ограниченной интересующей зоне.Во-первых, использование подхода ADER Discontinuous Galerkin (ADER-DG) высокого порядка во всей вычислительной области является дорогостоящим, поскольку не везде требуется высокий порядок точности. На самом деле, мелкие элементы уже могут обеспечивать достаточную точность благодаря их хорошему пространственному разрешению задачи. В этом случае подход ADER конечного объема (FV) высокого порядка (Dumbser et al. 2006b) может быть выгодным, поскольку вычислительные затраты на данной сетке меньше, чем для ADER-DG.Во-вторых, несколько наименьших элементов в сетке сокращают допустимый временной шаг для всех элементов сетки. Обычно такие ограничения временного шага применяются ко всем явным численным методам из-за проблем со стабильностью.
Обычно такие ограничения временного шага применяются ко всем явным численным методам из-за проблем со стабильностью.
Кроме того, автоматическое создание неструктурированной сетки может привести к чрезвычайно маленьким и вырожденным тетраэдрам, так называемым осколкам (Bern & Eppstein 1992; Joe 1995; Fleischmann et al. 1999). Лента характеризуется четырьмя вершинами, которые лежат почти в плоскости и, следовательно, приводят к очень плоскому тетраэдрическому элементу объема, почти равного нулю.Это явление хорошо известно в литературе по созданию неструктурированных трехмерных сеток. Его часто можно избежать, но не всегда (Cheng et al. 2000; Edelsbrunner & Guoy 2002). Однако при наличии таких вырожденных элементов качество численного решения в их окрестности может быть снижено и, что более важно, резко ограничен шаг по времени для явных численных методов. В крайних случаях может даже стать практически невозможным запуск численной схемы с разумным шагом по времени на сетке, содержащей ленточный элемент.
В этой статье мы предлагаем новую p -адаптивную схему ADER-DG с локальным временным шагом (LTS) для преодоления двух вышеупомянутых проблем, возникающих для реалистичных моделей сложной геометрии. Работа представляет собой важное расширение и улучшение схемы ADER-DG для задач распространения сейсмических волн, представленной в Käser & Dumbser (2006), Dumbser & Käser (2006) и Käser et al. (2007 г.). Подобно подходу Houston & Süli (2001), предложенная схема ADER-DG допускает локально различные полиномиальные степени численной аппроксимации внутри каждого элемента и, следовательно, обеспечивает лучший баланс точности и вычислительных затрат.
Кроме того, новый метод ADER-DG применяет метод LTS, так что в каждом элементе можно использовать максимальный временной шаг в соответствии с локальным критерием устойчивости. Благодаря подходу интегрирования времени ADER (Toro et al. 2001; Titarev & Toro 2002; Toro & Titarev 2002) для вычисления пространственно-временных потоков высокого порядка, метод остается одношаговой схемой с точностью по времени , несмотря ЛТС. LTS в сочетании со схемами DG на неструктурированных трехмерных сетках уже был предложен Flaherty et al. (1997). Однако они представили только результаты первого порядка. LTS для методов FV на неструктурированных тетраэдрических сетках был разработан Fumeaux et al. (2004 г.). Однако их подход не выходит за пределы второго порядка по пространству и времени. Отметим, что расширение этих предыдущих подходов на более высокий порядок во времени, например, с использованием метода временных шагов Рунге-Кутты (РК), было бы очень затратным с точки зрения памяти и процессорного времени из-за необходимости хранения промежуточного РК. этапы.Кроме того, требуется шаг интерполяции по времени для синхронизации этапов РК между разными элементами. Кроме того, эффективность схем временной дискретизации РК резко снижается, если порядок точности становится выше четвертого из-за так называемых барьеров Мясника (Бутчер, 1987), а количество промежуточных ступеней РК становится даже больше формального порядка точности.
LTS в сочетании со схемами DG на неструктурированных трехмерных сетках уже был предложен Flaherty et al. (1997). Однако они представили только результаты первого порядка. LTS для методов FV на неструктурированных тетраэдрических сетках был разработан Fumeaux et al. (2004 г.). Однако их подход не выходит за пределы второго порядка по пространству и времени. Отметим, что расширение этих предыдущих подходов на более высокий порядок во времени, например, с использованием метода временных шагов Рунге-Кутты (РК), было бы очень затратным с точки зрения памяти и процессорного времени из-за необходимости хранения промежуточного РК. этапы.Кроме того, требуется шаг интерполяции по времени для синхронизации этапов РК между разными элементами. Кроме того, эффективность схем временной дискретизации РК резко снижается, если порядок точности становится выше четвертого из-за так называемых барьеров Мясника (Бутчер, 1987), а количество промежуточных ступеней РК становится даже больше формального порядка точности. .
.
Напротив, использование подхода ADER имеет два преимущества: во-первых, это одноэтапная схема, поэтому не нужно сохранять промежуточные этапы RK.Во-вторых, временная интерполяция на границах раздела элементов естественным образом обеспечивается процедурой Коши-Ковалевского и, следовательно, не требует дополнительной интерполяции. Совсем недавно аналогичная схема РГ с использованием процедуры Коши-Ковалевского для пространственно-временного расширения и LTS была введена (Loercher et al. 2007) для нелинейных систем в одном пространственном измерении.
Структура этой статьи выглядит следующим образом. Во-первых, мы даем краткое введение в уравнения, управляющие распространением сейсмических волн в разделе 2.Затем p -адаптивная схема ADER-DG с LTS описана для этого типа уравнения в разделе 3. Подробное обсуждение алгоритма LTS следует в разделе 3.3. Чтобы продемонстрировать свойства численной сходимости схемы LTS, результаты для нескольких типов сеток показаны в разделе 4. Различные приложения предложенной схемы представлены в разделе 5. Первое приложение имеет дело со стандартным слоем над полупространством (LOH. 1) тестовый пример, для которого доступны аналитические и численные эталонные решения.Второй тестовый пример представляет собой трехмерное расширение тестового примера жесткого включения, предложенного в двух пространственных измерениях LeVeque (2002). Наконец, представлен реалистичный пример моделирования землетрясений и прогнозирования движения грунта в альпийской долине Гренобля, где используются все возможности адаптивной схемы ADER-DG p с LTS на неструктурированных тетраэдрических сетках.
Различные приложения предложенной схемы представлены в разделе 5. Первое приложение имеет дело со стандартным слоем над полупространством (LOH. 1) тестовый пример, для которого доступны аналитические и численные эталонные решения.Второй тестовый пример представляет собой трехмерное расширение тестового примера жесткого включения, предложенного в двух пространственных измерениях LeVeque (2002). Наконец, представлен реалистичный пример моделирования землетрясений и прогнозирования движения грунта в альпийской долине Гренобля, где используются все возможности адаптивной схемы ADER-DG p с LTS на неструктурированных тетраэдрических сетках.
2 Уравнения упругих волн
Распространение волн в упругой среде основано на теории линейной упругости (Бедфорд и Драмхеллер, 1994; Аки и Ричардс, 2002), которая приводит к следующей гиперболической системе в формулировке скорости-напряжения: константы и ρ — массовая плотность материала. Нормальные компоненты стресса даны Σ x x , Σ yy и Σ ZZ , а подстреки сдвига σ x Y , Σ yz и σ xz . Компоненты скоростей частиц в направлениях х , y и z обозначаются u , v и w соответственно. Эта система является естественным расширением двумерной системы, которая уже использовалась в основополагающих работах Virieux (1984, 1986).
Нормальные компоненты стресса даны Σ x x , Σ yy и Σ ZZ , а подстреки сдвига σ x Y , Σ yz и σ xz . Компоненты скоростей частиц в направлениях х , y и z обозначаются u , v и w соответственно. Эта система является естественным расширением двумерной системы, которая уже использовалась в основополагающих работах Virieux (1984, 1986).Заметим, что для простоты обозначений мы опускаем зависимости переменных от времени и пространства, т. е. в оставшейся части статьи напряжения и скорости всегда предполагаются функциями времени и пространства. Физические свойства материала являются функциями пространства, но постоянны во времени, то есть и , чтобы описать гетерогенный материал.
в следующем, мы пишем систему (2) в более компактной форме 2 где Q P = (Σ x x , Σ YY , Σ ZZ , Σ x Y , Σ , Σ yz , Σ xz , U , V , W ) T — вектор неизвестных переменных системы. Обратите внимание, что используется классическая тензорная запись, которая подразумевает суммирование по каждому индексу, который встречается дважды. Матрицы и являются зависящими от пространства матрицами Якоби размера p × q , где p , q = 1, …, 9, и приведены, например, в Dumbser & Käser (2006). Для неупругого случая, включая вязкоупругое затухание (см. Käser et al. 2007), подробности о схемах ADER-DG для анизотропного материала можно найти в de la Puente et al. (2006 г.).
Обратите внимание, что используется классическая тензорная запись, которая подразумевает суммирование по каждому индексу, который встречается дважды. Матрицы и являются зависящими от пространства матрицами Якоби размера p × q , где p , q = 1, …, 9, и приведены, например, в Dumbser & Käser (2006). Для неупругого случая, включая вязкоупругое затухание (см. Käser et al. 2007), подробности о схемах ADER-DG для анизотропного материала можно найти в de la Puente et al. (2006 г.).3 Схема Ader-Dg с
P — Адаптивность и локальное время Stepping Для построения численной схемы рассмотрим общую линейную гиперболическую систему уравнений с переменными коэффициентами вида (2). Вычислительная область разделена на соответствующие тетраэдрические элементы T ( m ) , адресованные уникальным индексом ( m ). Кроме того, мы предполагаем матрицы рд , Б рд и С рд постоянной кусочно внутри элемента Т ( м ) .
3.1 Полудискретная
р — адаптивная схема Численное решение уравнения. (2) аппроксимируется внутри каждого тетраэдра T ( m ) линейной комбинацией зависящих от пространства, но не зависящих от времени полиномиальных базисных функций Φ l (ξ, η, ζ) степени N с опорой T ( m ) и с зависящими от времени степенями свободы следующим образом: 3 где ξ, η и ζ — координаты в базовой системе координат.Связь между физическими координатами x – y – z и базовой системой координат ξ−η−ζ представляет собой простое линейное отображение (см., например, Dumbser & Käser 2006). Это отображение преобразует физический тетраэдр T ( m ) в канонический опорный элемент T E с четырьмя вершинами (0, 0, 0), (1, 0, 0) (0 , 1, 0) и (0, 0, 1). В уравнении (3) индекс p обозначает количество неизвестных в векторе Q , а l указывает на l -ю базисную функцию.Мы используем иерархические ортогональные базисные функции Φ k , как указано в Cockburn et al. (2000). Иерархический означает, что степени свободы упорядочены по порядку относительно степени полинома, начиная с низшей степени (многочлены нулевой степени) до высшей. В трех пространственных измерениях для элемента, использующего базисные функции максимальной степени N , индекс l изменяется от 1 до числа степеней свободы .Для p -адаптивной версии схемы локальная степень базисных полиномов может меняться от элемента к элементу и, таким образом, N становится функцией номера элемента ( m ). Поэтому мы пишем N = N ( м ) = N ( T ( м ) ). Отметим, в частности, что из-за ортогональности базисных функций полиномиальное приближение более низкого порядка может быть получено из полиномиального приближения более высокого порядка, просто установив степени свободы, соответствующие высшим полиномиальным степеням, равными нулю.
В уравнении (3) индекс p обозначает количество неизвестных в векторе Q , а l указывает на l -ю базисную функцию.Мы используем иерархические ортогональные базисные функции Φ k , как указано в Cockburn et al. (2000). Иерархический означает, что степени свободы упорядочены по порядку относительно степени полинома, начиная с низшей степени (многочлены нулевой степени) до высшей. В трех пространственных измерениях для элемента, использующего базисные функции максимальной степени N , индекс l изменяется от 1 до числа степеней свободы .Для p -адаптивной версии схемы локальная степень базисных полиномов может меняться от элемента к элементу и, таким образом, N становится функцией номера элемента ( m ). Поэтому мы пишем N = N ( м ) = N ( T ( м ) ). Отметим, в частности, что из-за ортогональности базисных функций полиномиальное приближение более низкого порядка может быть получено из полиномиального приближения более высокого порядка, просто установив степени свободы, соответствующие высшим полиномиальным степеням, равными нулю. Это станет важным позже при вычислении потоков между элементами разной степени локального полинома.
Это станет важным позже при вычислении потоков между элементами разной степени локального полинома. Подчеркнем, что из-за иерархических ортогональных базисных функций ур. (4) уже содержит полностью p -адаптивный случай. Нужно только обратить внимание на диапазон индексов при вычислении потока через грани элемента. Индексы k и l всегда находятся в диапазоне от 1 до локального числа степеней свободы внутри элемента ( m ), то есть 1 ≤ k ≤ N d [ N . m ) ] и 1 ≤ l ≤ N d [ N ( m ) ].Однако для вкладов потока соседнего элемента ( k j ) через грань j максимум степеней полинома в элементе ( m ) и соседе ( k ) ) нужно взять. Объяснение этому очень простое: в схеме ADER-DG численный поток основан на решении обобщенных задач Римана (GRP) на границах раздела элементов, которые состоят из кусочно-полиномиальных начальных условий, разделенных разрывом на границе раздела элементов ( Титарев и Торо, 2002). Степень GRP определяется максимальной степенью полинома, возникающей на любой из двух сторон интерфейса, поскольку полиномы более низкой степени являются лишь частными случаями полиномов более высокой степени. Следовательно, индекс n находится внутри диапазона. Недостающие степени свободы в элементе нижнего порядка необходимо заполнить нулями. Это означает, что матрицы потоков и матрицы жесткости должны вычисляться до максимальной полиномиальной степени, возникающей во всей расчетной области.Тогда для каждого элемента нужно рассматривать только соответствующие подматрицы до нужной степени. Для вкладов потоков соседних элементов эти подматрицы могут быть прямоугольными, когда необходимо вычислить потоки между двумя элементами различной полиномиальной степени N . Для удобства храним для каждого элемента все степени свободы вплоть до максимальной полиномиальной степени, возникающей во всей расчетной области, полагая нулевыми те степени свободы, степень которых превышает локальную полиномиальную степень внутри элемента.
Степень GRP определяется максимальной степенью полинома, возникающей на любой из двух сторон интерфейса, поскольку полиномы более низкой степени являются лишь частными случаями полиномов более высокой степени. Следовательно, индекс n находится внутри диапазона. Недостающие степени свободы в элементе нижнего порядка необходимо заполнить нулями. Это означает, что матрицы потоков и матрицы жесткости должны вычисляться до максимальной полиномиальной степени, возникающей во всей расчетной области.Тогда для каждого элемента нужно рассматривать только соответствующие подматрицы до нужной степени. Для вкладов потоков соседних элементов эти подматрицы могут быть прямоугольными, когда необходимо вычислить потоки между двумя элементами различной полиномиальной степени N . Для удобства храним для каждого элемента все степени свободы вплоть до максимальной полиномиальной степени, возникающей во всей расчетной области, полагая нулевыми те степени свободы, степень которых превышает локальную полиномиальную степень внутри элемента. Это увеличивает память компьютера, но упрощает вычисление потоков для элементов с разной полиномиальной степенью.
Это увеличивает память компьютера, но упрощает вычисление потоков для элементов с разной полиномиальной степенью.
Наконец, мы хотели бы отметить, что дальнейшие подробности построения схемы ADER-DG для уравнений упругих волн в двух и трех пространственных измерениях можно найти в Käser & Dumbser (2006), Dumbser & Käser (2006), Кезер и др. (2007 г.) и de la Puente и др. (2006), где также можно найти подробную информацию об обработке типичных граничных условий, таких как свободная поверхность и открытые граничные условия.
3.2 Шаг по локальному времени с использованием подхода ADER-DG
Эффективность схем временной дискретизации РК резко снижается, если порядок точности становится больше четвертого из-за так называемых барьеров Мясника (Бутчер, 1987), а количество промежуточных ступеней РК становится больше формального порядка точности. Поэтому мы применяем подход АДЭР к полудискретной форме ДР-схемы (4), чтобы добиться такой же точности дискретизации по времени, как и для дискретизации по пространству. Кроме того, точный по времени LTS высокого порядка точности стал бы довольно сложным со схемами RK, поскольку внутри подхода LTS промежуточные уровни времени RK двух соседних элементов в общем случае не совпадают. Это делает необходимой точную временную интерполяцию между элементами. Конечно, LTS-версия предлагаемого подхода ADER-DG также нуждается в точной временной интерполяции. Однако это естественно вытекает из построения метода благодаря использованию процедуры Коши-Ковалевского, обеспечивающей точное предсказание эволюции степеней свободы каждого элемента в течение одного временного шага.
Кроме того, точный по времени LTS высокого порядка точности стал бы довольно сложным со схемами RK, поскольку внутри подхода LTS промежуточные уровни времени RK двух соседних элементов в общем случае не совпадают. Это делает необходимой точную временную интерполяцию между элементами. Конечно, LTS-версия предлагаемого подхода ADER-DG также нуждается в точной временной интерполяции. Однако это естественно вытекает из построения метода благодаря использованию процедуры Коши-Ковалевского, обеспечивающей точное предсказание эволюции степеней свободы каждого элемента в течение одного временного шага.
Основным компонентом подхода ADER является решение обобщенных задач Римана (GRP) (Toro et al. 2001), которое принимает форму разложения в ряд Тейлора во времени. Затем процедура Коши-Ковалевского используется для замены производных по времени в ряду Тейлора производными по пространству. Поскольку состояние и пространственные производные, как правило, разрывны на границах раздела элементов, их значение на границе определяется решением задач Римана для состояния и пространственных производных (см. также Торо и Титарев, 2002).Формально полностью дискретная схема с использованием LTS аналогична схемам ADER-DG с глобальным шагом по времени, представленным в Dumbser & Munz (2005); Кезер и Тумбсер (2006); Dumbser & Käser (2006), однако тензор интегрирования по времени I plqm должен быть рассчитан с учетом локального алгоритма шага по времени.
также Торо и Титарев, 2002).Формально полностью дискретная схема с использованием LTS аналогична схемам ADER-DG с глобальным шагом по времени, представленным в Dumbser & Munz (2005); Кезер и Тумбсер (2006); Dumbser & Käser (2006), однако тензор интегрирования по времени I plqm должен быть рассчитан с учетом локального алгоритма шага по времени.
1 м
) .Критерий стабильности для локального временного шага записывается как 9, где l ( m ) min — диаметр внутренней сферы тетраэдра T ( m ) and m ) max — максимальная скорость сигнала, возникающего в тетраэдре. A ( м ) MAX — максимальное собственное значение jacobians A PQ , B PQ и C PQ , что означает для Изотропные упругие волновые уравнения A ( м ) MAX = C P P , локальный сейсмический P -волная скорость в тетраэдроне T ( м ) . Наиболее важными уравнениями для алгоритма LTS являются критерий обновления элементов и временной интервал для расчета потока. Элемент может быть обновлен тогда и только тогда, когда критерий обновления 15 выполняется в отношении всех непосредственно соседних тетраэдров. Когда элемент обновляется, выполняя (15), числовые потоки между двумя элементами T ( m ) и должны быть вычислены во временном интервале 16 Аналогично случаю глобального шага по времени, представленному, например, в Käser & Dumbser (2006) и dumbser & käser (2006), представим определение 17 с 18, где I PLQM ( T 0 , T 1 , T 2 ) формально содержит процедуру Коши-Ковалевского для интервала времени t ∈[ t 1 ; t 2 ] с рядом Тейлора, расширенным около уровня времени t 0 .С учетом (18) полностью дискретная p -адаптивная LTS-схема ADER-DG задается при условии (15) формулой: как подробно описано для полудискретной p -адаптивной схемы (4).
Наиболее важными уравнениями для алгоритма LTS являются критерий обновления элементов и временной интервал для расчета потока. Элемент может быть обновлен тогда и только тогда, когда критерий обновления 15 выполняется в отношении всех непосредственно соседних тетраэдров. Когда элемент обновляется, выполняя (15), числовые потоки между двумя элементами T ( m ) и должны быть вычислены во временном интервале 16 Аналогично случаю глобального шага по времени, представленному, например, в Käser & Dumbser (2006) и dumbser & käser (2006), представим определение 17 с 18, где I PLQM ( T 0 , T 1 , T 2 ) формально содержит процедуру Коши-Ковалевского для интервала времени t ∈[ t 1 ; t 2 ] с рядом Тейлора, расширенным около уровня времени t 0 .С учетом (18) полностью дискретная p -адаптивная LTS-схема ADER-DG задается при условии (15) формулой: как подробно описано для полудискретной p -адаптивной схемы (4). Кроме того, моменты времени t 1 и t 2 обозначают пределы временного интервала потока и задаются согласно (16). Точная интерполяция временных уровней элемента, необходимая для согласованного расчета потока, выполняется автоматически с помощью процедуры Коши-Ковалевского с использованием (17) с (18).Отметим, что вклады матриц жесткости всегда рассчитываются для полного локального временного шага ∆ t m , поскольку интегралы по объему зависят только от локальной информации элемента.
Кроме того, моменты времени t 1 и t 2 обозначают пределы временного интервала потока и задаются согласно (16). Точная интерполяция временных уровней элемента, необходимая для согласованного расчета потока, выполняется автоматически с помощью процедуры Коши-Ковалевского с использованием (17) с (18).Отметим, что вклады матриц жесткости всегда рассчитываются для полного локального временного шага ∆ t m , поскольку интегралы по объему зависят только от локальной информации элемента.Однако, поскольку потоки, вычисленные для элемента T ( m ) в интервале (16), вообще говоря, не покрывают весь локальный временной шаг, все остальные вклады потоков должны вычисляться соседними элементами, когда они удовлетворяют критерий обновления (15).Другими словами, интеграл потока за весь интервал времени [ t ( м ) ; t ( m ) +Δ t ( m ) ] разбивается на собственный вклад элемента в подинтервале [ t
1 ; t 2 ] и вклады соответствующего соседнего элемента в остальной части интервала. Эти вклады соседей могут исходить от нескольких локальных временных шагов соседа.Для этого соседи добавляют свои соответствующие вклады потока в так называемую переменную памяти потока для тетраэдра T ( m ) . Мы подчеркиваем, что переменные памяти потока используются для хранения вкладов потока соседних элементов и что их не следует путать с обычными переменными памяти, используемыми для моделирования неупругого затухания. В начальный момент времени t = 0 все переменные памяти потока инициализируются нулем. После выполнения локального временного шага элемента в соответствии с (19) переменная памяти потока самого элемента обнуляется, и приращения, которые должны быть добавлены к переменным памяти потока всех его соседей, вычисляются следующим образом: 20 Вместо использования тензора, приведенного в (18), в качестве альтернативы можно использовать более быстрый алгоритм, приведенный в приложении Käser et al. (2007) и сохранить полученный временной ряд Тейлора для каждой степени свободы в каждом элементе.
Эти вклады соседей могут исходить от нескольких локальных временных шагов соседа.Для этого соседи добавляют свои соответствующие вклады потока в так называемую переменную памяти потока для тетраэдра T ( m ) . Мы подчеркиваем, что переменные памяти потока используются для хранения вкладов потока соседних элементов и что их не следует путать с обычными переменными памяти, используемыми для моделирования неупругого затухания. В начальный момент времени t = 0 все переменные памяти потока инициализируются нулем. После выполнения локального временного шага элемента в соответствии с (19) переменная памяти потока самого элемента обнуляется, и приращения, которые должны быть добавлены к переменным памяти потока всех его соседей, вычисляются следующим образом: 20 Вместо использования тензора, приведенного в (18), в качестве альтернативы можно использовать более быстрый алгоритм, приведенный в приложении Käser et al. (2007) и сохранить полученный временной ряд Тейлора для каждой степени свободы в каждом элементе. Это увеличивает скорость вычислений за счет более высоких требований к памяти.
Это увеличивает скорость вычислений за счет более высоких требований к памяти.Особенностью предлагаемой p -адаптивной схемы АДЭР-ДГ является ее p -адаптивность не только в пространстве, но и во времени . Это происходит автоматически с помощью процедуры Коши-Ковалевски, которая автоматически сопоставляет пространственную и временную точность. Это было бы довольно сложно получить с помощью схемы РК РГ, так как использование схем РК с локально разным порядком точности потребовало бы дополнительной интерполяции на интерфейсах элементов, поскольку временные уровни промежуточных стадий РК не обязательно совпадают.Поэтому мы решили назвать нашу схему ADER-DG p τ -адаптивной, указав, что она адаптирует степень локального полинома не только в пространстве, но и во времени.
3.3 Обсуждение алгоритма локального шага по времени
В этом разделе мы хотели бы подробно проиллюстрировать алгоритм, заданный формулами (19) и (20) при условиях (15) и (16), на схематическом одномерном примере. Рассмотрим пять неравноудаленных элементов от T (1) до T (5) , как показано на рис.1 со связанными с ними различными локальными временными шагами от Δ t (1) до Δ t (5) , как показано на рис. 1(a). Предположим, что все элементы начинаются с одного и того же общего уровня времени t = 0 и что все они должны достичь одного и того же конечного времени вывода t = t o . Поскольку для LTS-алгоритма продвижение элементов во времени не будет синхронным, в дальнейшем мы будем говорить о «циклах», которые определим следующим образом: в течение одного цикла только подмножество всех элементов T ( m ) который выполняет (15) обновляется.Возвращаясь к нашему примеру, показанному на рис. 1, мы видим, что в первом цикле только элементы T (3) и T (5) удовлетворяют критерию обновления (15).
Рассмотрим пять неравноудаленных элементов от T (1) до T (5) , как показано на рис.1 со связанными с ними различными локальными временными шагами от Δ t (1) до Δ t (5) , как показано на рис. 1(a). Предположим, что все элементы начинаются с одного и того же общего уровня времени t = 0 и что все они должны достичь одного и того же конечного времени вывода t = t o . Поскольку для LTS-алгоритма продвижение элементов во времени не будет синхронным, в дальнейшем мы будем говорить о «циклах», которые определим следующим образом: в течение одного цикла только подмножество всех элементов T ( m ) который выполняет (15) обновляется.Возвращаясь к нашему примеру, показанному на рис. 1, мы видим, что в первом цикле только элементы T (3) и T (5) удовлетворяют критерию обновления (15). Таким образом, в цикле 1 им разрешено выполнять обновление. Для вычисления потоков значения соседних элементов интерполируются с помощью процедуры Коши-Ковалевского благодаря (18) в интервалах, определяемых (16). Более подробно это обсуждается на примере элемента T (3) и его соседей далее.Интервалы времени, в которых выполняется вычисление потока согласно (16), составляют [ a ; b ] на интерфейсе с соседом T (2) и [ h ; i ] на интерфейсе с соседом T (4) . Переменные памяти потока и обоих соседей обновляются согласно (20). В цикле 2 только T (2) и T (5) могут выполнять обновление, см. также рис.1(с). Согласно (16), поток между T (2) и T (3) необходимо вычислять только во временном интервале [ b ; c ] поскольку поток в интервале [ a ; b ] уже было вычислено в цикле 1 соседним элементом T (3) .
Таким образом, в цикле 1 им разрешено выполнять обновление. Для вычисления потоков значения соседних элементов интерполируются с помощью процедуры Коши-Ковалевского благодаря (18) в интервалах, определяемых (16). Более подробно это обсуждается на примере элемента T (3) и его соседей далее.Интервалы времени, в которых выполняется вычисление потока согласно (16), составляют [ a ; b ] на интерфейсе с соседом T (2) и [ h ; i ] на интерфейсе с соседом T (4) . Переменные памяти потока и обоих соседей обновляются согласно (20). В цикле 2 только T (2) и T (5) могут выполнять обновление, см. также рис.1(с). Согласно (16), поток между T (2) и T (3) необходимо вычислять только во временном интервале [ b ; c ] поскольку поток в интервале [ a ; b ] уже было вычислено в цикле 1 соседним элементом T (3) . Поскольку этот вклад был сохранен в переменной памяти потока T (2) , теперь он правильно учитывается на этапе обновления для T (2) .Вклад потока элемента T (2) в его соседа T (3) аналогичным образом добавляется к переменной памяти потока соседа T (3) . Помните, что в конце цикла обнуляется. Аналогичным образом T (5) добавит свой вклад потока в переменные памяти потока элемента T (4) . В цикле 3 кроме T (5) также элемент T (3) снова выполняет условие (15), см. рис.1(d), и вычисляет потоки во временном интервале [ c ; d ] на границе с соседом T (2) с момента вклада интервала [ b ; c ] уже было вычислено в цикле 2 с помощью T (2) и сохранено в . По отношению к соседу T (4) поток вычисляется по (16) в интервале [ i ; j ], что, очевидно, способствует обновлению элемента T (3) , а также соответствующему обновлению переменной памяти потока .
Поскольку этот вклад был сохранен в переменной памяти потока T (2) , теперь он правильно учитывается на этапе обновления для T (2) .Вклад потока элемента T (2) в его соседа T (3) аналогичным образом добавляется к переменной памяти потока соседа T (3) . Помните, что в конце цикла обнуляется. Аналогичным образом T (5) добавит свой вклад потока в переменные памяти потока элемента T (4) . В цикле 3 кроме T (5) также элемент T (3) снова выполняет условие (15), см. рис.1(d), и вычисляет потоки во временном интервале [ c ; d ] на границе с соседом T (2) с момента вклада интервала [ b ; c ] уже было вычислено в цикле 2 с помощью T (2) и сохранено в . По отношению к соседу T (4) поток вычисляется по (16) в интервале [ i ; j ], что, очевидно, способствует обновлению элемента T (3) , а также соответствующему обновлению переменной памяти потока . В следующем цикле 4 элементы T (2) и T (5) выполняют обновление времени, см. рис. 1(e). Интервал времени потока на интерфейсах между T (2) и T (3) теперь составляет [ d ; и ]. T (1) удовлетворяет критерию обновления впервые в цикле 5, см. рис. 1(f). В циклах 6–8 обновляется только наименьший элемент T (5) , поскольку ни один из других элементов не удовлетворяет критерию обновления.Эта процедура LTS продолжается таким образом до цикла 22, когда все элементы достигли конечного времени вывода t o , см. рис. 1(f)–(p). Особый интерес представляет цикл 11, в котором соседние элементы T (2) и T (3) одновременно удовлетворяют критерию обновления, поскольку они достигают общего уровня местного времени, скажем, t c . Мы хотим использовать этот пример, чтобы проиллюстрировать, как работает шаг по локальному времени в этом особом случае.
В следующем цикле 4 элементы T (2) и T (5) выполняют обновление времени, см. рис. 1(e). Интервал времени потока на интерфейсах между T (2) и T (3) теперь составляет [ d ; и ]. T (1) удовлетворяет критерию обновления впервые в цикле 5, см. рис. 1(f). В циклах 6–8 обновляется только наименьший элемент T (5) , поскольку ни один из других элементов не удовлетворяет критерию обновления.Эта процедура LTS продолжается таким образом до цикла 22, когда все элементы достигли конечного времени вывода t o , см. рис. 1(f)–(p). Особый интерес представляет цикл 11, в котором соседние элементы T (2) и T (3) одновременно удовлетворяют критерию обновления, поскольку они достигают общего уровня местного времени, скажем, t c . Мы хотим использовать этот пример, чтобы проиллюстрировать, как работает шаг по локальному времени в этом особом случае. В начале цикла оба элемента находятся на разных уровнях местного времени t c −Δ t (2) и t c −Δ t 1 (2) и t c −Δ t 1 Предположим, что в цикле 11 алгоритм сначала рассматривает элемент T (2) для обновления. Это означает, что поток интерфейса будет вычисляться с помощью T (2) , обновляя переменную памяти потока. Элемент T (2) впоследствии достигает времени t c .Когда наступает очередь T (3) обновляться в том же цикле, поток на общем интерфейсе уже рассчитан его соседом. Это правильно соблюдается интервалом времени потока (16), начиная с t 1 = max [ t (2) , t (3) ]= t ]= t 9012
В начале цикла оба элемента находятся на разных уровнях местного времени t c −Δ t (2) и t c −Δ t 1 (2) и t c −Δ t 1 Предположим, что в цикле 11 алгоритм сначала рассматривает элемент T (2) для обновления. Это означает, что поток интерфейса будет вычисляться с помощью T (2) , обновляя переменную памяти потока. Элемент T (2) впоследствии достигает времени t c .Когда наступает очередь T (3) обновляться в том же цикле, поток на общем интерфейсе уже рассчитан его соседом. Это правильно соблюдается интервалом времени потока (16), начиная с t 1 = max [ t (2) , t (3) ]= t ]= t 9012
 Интервал времени [ t 1 ; t 2 ]=[ t c ; t c ] становится сингулярной и, следовательно, из T (3) не получается никакого дополнительного расчета потока. Те же рассуждения верны для другого порядка расположения обоих элементов, то есть если сначала элемент T (3) планируется обновить, а затем элемент T (2) . Обратите внимание, что за исключением конечных временных шагов и промежуточных выходных времен, где временные шаги всех локальных элементов корректируются для достижения точного значения t o , синхронизация не используется.
Интервал времени [ t 1 ; t 2 ]=[ t c ; t c ] становится сингулярной и, следовательно, из T (3) не получается никакого дополнительного расчета потока. Те же рассуждения верны для другого порядка расположения обоих элементов, то есть если сначала элемент T (3) планируется обновить, а затем элемент T (2) . Обратите внимание, что за исключением конечных временных шагов и промежуточных выходных времен, где временные шаги всех локальных элементов корректируются для достижения точного значения t o , синхронизация не используется.Рисунок 1.
Иллюстрация алгоритма шага по локальному времени в одном пространственном измерении, показывающая пространственно-временные элементы.
Рис. 1.
Иллюстрация алгоритма шага по локальному времени в одном пространственном измерении, показывающая пространственно-временные элементы.
Наконец, мы хотели бы проиллюстрировать преимущества алгоритма LTS, обсуждая рис. 2. Слева мы видим обычную процедуру обновления элементов для глобальной схемы временного шага.Временной шаг всех элементов ограничивается наименьшим из возникающих во всей расчетной области. В нашем примере это Δ t (5) , что приводит к общему количеству обновлений элементов 100. Для задач, зависящих от времени, решение зависит как от пространства, так и от времени, и поэтому, когда решение продвигается во времени, окончательная сетка является не только пространственной, но и пространственно-временной сеткой. Это показано на рис. 2, где показаны пространственная сетка в направлении x и временная сетка в направлении t .Поскольку для глобальной схемы временного шага нет висячих узлов во времени, сетка называется конформной. Вместо 100 обновлений элементов мы также можем сказать, что метод использует пространственно-временную сетку со 100 соответствующими пространственно-временными элементами. Для LTS-схемы размер сетки по времени определяется оптимальным образом, поскольку каждый элемент может работать с максимальным шагом по времени, допускаемым критерием устойчивости (9). Это, однако, приводит к несоответствующей сетке с висячими узлами во времени. Чтобы иметь дело с этими висячими узлами, была введена концепция переменных памяти потока, поскольку интеграл потока во времени является линейно аддитивным.Результирующая пространственно-временная сетка для LTS-схемы содержит всего 37 пространственно-временных элементов. Она более сложна по структуре, чем соответствующая сетка глобальной схемы шага по времени со 100 пространственно-временными элементами, но требует меньших вычислительных затрат.
Для LTS-схемы размер сетки по времени определяется оптимальным образом, поскольку каждый элемент может работать с максимальным шагом по времени, допускаемым критерием устойчивости (9). Это, однако, приводит к несоответствующей сетке с висячими узлами во времени. Чтобы иметь дело с этими висячими узлами, была введена концепция переменных памяти потока, поскольку интеграл потока во времени является линейно аддитивным.Результирующая пространственно-временная сетка для LTS-схемы содержит всего 37 пространственно-временных элементов. Она более сложна по структуре, чем соответствующая сетка глобальной схемы шага по времени со 100 пространственно-временными элементами, но требует меньших вычислительных затрат.
Рисунок 2.
Сравнение результирующих пространственно-временных сеток с использованием глобального временного шага (слева) и локального временного шага (справа).
Рисунок 2.
Сравнение результирующих пространственно-временных сеток с использованием глобального временного шага (слева) и локального временного шага (справа).
В отличие от пространственно-временного DG-подхода (van der Vegt & van der Ven 2002), который является неявным во времени и базисные функции которого зависят как от пространства, так и от времени, наш алгоритм остается явным во времени с базисными функциями, зависящими только от космос. Пространственно-временной характер схем ADER-DG проявляется непосредственно через процедуру Коши-Ковалевского и ряд Тейлора по времени в уравнении. (12). Подчеркнем, что по сравнению с пространственно-временной DG-схемой ван дер Вегта и ван дер Вена (2002) наш алгоритм ADER-DG требует меньшего количества базисных функций при той же полиномиальной степени, поскольку на трехмерных сетках их подход приводит к четырехмерной сетке. полиномиальный базис.
Следует отметить, что общие накладные расходы, связанные с алгоритмом LTS, очень малы по сравнению со схемой ADER-DG, использующей глобальное временное пошаговое выполнение. Вычисления с последовательным кодом на трехмерных тетраэдральных сетках показали накладные расходы всего около 15%. Обратите внимание, однако, что эффективное параллельное выполнение схемы LTS может стать очень сложной задачей. Поскольку каждый элемент выполняет свое обновление только тогда, когда (15) выполняется локально, обновления элементов, как правило, полностью асинхронны, что приводит к очень неравномерному распределению нагрузки на разные процессоры.Поэтому для параллельной реализации нашего кода мы сначала группируем элементы зон со схожими свойствами материала и размерами элементов вместе и разбиваем каждую из этих зон отдельно на количество разделов, равное общему количеству процессоров. Для этой цели мы используем бесплатный программный пакет METIS, представленный Кариписом и Кумаром (1998). Затем полученные разделы разных зон объединяются вместе и таким образом обеспечивают окончательную декомпозицию домена. Обратите внимание, что последний раздел обычно содержит несвязанные поддомены.Однако, поскольку подход ADER-DG предусматривает одношаговую схему, общие коммуникационные издержки, вызванные этими несмежными разделами, довольно малы по сравнению с достигнутыми преимуществами улучшенной балансировки нагрузки.
Обратите внимание, однако, что эффективное параллельное выполнение схемы LTS может стать очень сложной задачей. Поскольку каждый элемент выполняет свое обновление только тогда, когда (15) выполняется локально, обновления элементов, как правило, полностью асинхронны, что приводит к очень неравномерному распределению нагрузки на разные процессоры.Поэтому для параллельной реализации нашего кода мы сначала группируем элементы зон со схожими свойствами материала и размерами элементов вместе и разбиваем каждую из этих зон отдельно на количество разделов, равное общему количеству процессоров. Для этой цели мы используем бесплатный программный пакет METIS, представленный Кариписом и Кумаром (1998). Затем полученные разделы разных зон объединяются вместе и таким образом обеспечивают окончательную декомпозицию домена. Обратите внимание, что последний раздел обычно содержит несвязанные поддомены.Однако, поскольку подход ADER-DG предусматривает одношаговую схему, общие коммуникационные издержки, вызванные этими несмежными разделами, довольно малы по сравнению с достигнутыми преимуществами улучшенной балансировки нагрузки. Обратите внимание, что простое использование METIS для всего домена с большими весами для элементов с малыми временными шагами не может решить проблему, поскольку загрузка процессора может оставаться несбалансированной из-за асинхронных обновлений элементов. В качестве последнего замечания о распараллеливании мы хотели бы отметить, что в нашей реализации MPI-связь всегда выполняется после каждого цикла.
Обратите внимание, что простое использование METIS для всего домена с большими весами для элементов с малыми временными шагами не может решить проблему, поскольку загрузка процессора может оставаться несбалансированной из-за асинхронных обновлений элементов. В качестве последнего замечания о распараллеливании мы хотели бы отметить, что в нашей реализации MPI-связь всегда выполняется после каждого цикла.
 Общее количество пространственно-временных элементов N LTS STE в пространственно-временной области Ω× T для схемы LTS 21 Δ t 1 , поэтому соответствующее число пространственно-временных элементов равно 22. Теоретическое ускорение σ теперь дается как отношение числа пространственно-временных элементов в (22) и (21) и, наконец, может можно записать как 23. Чтобы понять эту формулу в более конкретном смысле, мы рассмотрим два крайних случая τ→∞, что имеет место при крайнем несоответствии двух временных шагов, и случай α→0, который имеет место, когда только пренебрежимо малое число элементов сетки должно использовать малый шаг по времени ∆ t 1 .В первом случае получаем 24, а во втором 25. Особенно важен первый результат (24) для практических приложений. В предельном случае чрезвычайно большого отношения шага по времени τ именно не отношение шага по времени определяет максимальное теоретическое ускорение, а процент α элементов, использующих малый шаг по времени Δ t 1 .
Общее количество пространственно-временных элементов N LTS STE в пространственно-временной области Ω× T для схемы LTS 21 Δ t 1 , поэтому соответствующее число пространственно-временных элементов равно 22. Теоретическое ускорение σ теперь дается как отношение числа пространственно-временных элементов в (22) и (21) и, наконец, может можно записать как 23. Чтобы понять эту формулу в более конкретном смысле, мы рассмотрим два крайних случая τ→∞, что имеет место при крайнем несоответствии двух временных шагов, и случай α→0, который имеет место, когда только пренебрежимо малое число элементов сетки должно использовать малый шаг по времени ∆ t 1 .В первом случае получаем 24, а во втором 25. Особенно важен первый результат (24) для практических приложений. В предельном случае чрезвычайно большого отношения шага по времени τ именно не отношение шага по времени определяет максимальное теоретическое ускорение, а процент α элементов, использующих малый шаг по времени Δ t 1 . Это означает, что, например, в вычислительной области, где 20 % элементов должны использовать малый шаг по времени Δ t 1 , максимальное ускорение не может превышать 5.Когда уже 50 % элементов должны использовать малый временной шаг, нельзя ожидать, что ускорение будет больше двух. Всегда следует помнить об этом важном результате при принятии решения об использовании алгоритма LTS или нет, особенно учитывая трудности с балансировкой нагрузки схем LTS на суперкомпьютерах с массовым параллелизмом.
Это означает, что, например, в вычислительной области, где 20 % элементов должны использовать малый шаг по времени Δ t 1 , максимальное ускорение не может превышать 5.Когда уже 50 % элементов должны использовать малый временной шаг, нельзя ожидать, что ускорение будет больше двух. Всегда следует помнить об этом важном результате при принятии решения об использовании алгоритма LTS или нет, особенно учитывая трудности с балансировкой нагрузки схем LTS на суперкомпьютерах с массовым параллелизмом. Коэффициент шага по времени τ определяет ускорение только в том случае, когда в области присутствует крайне мало элементов с малым шагом по времени ∆ t 1 (α→ 0).Например, это тот случай, когда тетраэдрическая сетка содержит только одну единственную щепку. Применение этого крайнего случая показано в следующем разделе 4.2, где мы показываем результаты сходимости, полученные с нашей схемой LTS на правильной тетраэдрической сетке, содержащей четыре полоски.
4 Численные исследования сходимости схемы Lts Ader-Dg
Здесь мы представляем результаты численного анализа сходимости, чтобы подтвердить равномерно высокую точность в пространстве и времени предложенного метода ADER-DG с точным по времени LTS.Порядки сходимости схем LTS ADER-DG показаны со второго по шестой порядок по пространству и времени и обозначены LTS ADER-DG до ADER-DG соответственно. Отметим, что схема АДЭР-ДГ с использованием базисных полиномов Φ l максимальной степени N имеет формальный порядок точности N + 1 в пространстве и времени. Это означает, что, например, метод ADER-DG использует базисные полиномы максимальной степени N = 5.
Затем мы произвольно выбираем одну из переменных системы упругой волны ур.2) численно определить порядок сходимости используемых схем LTS ADER-DG. В таблицах 1 и 3 приведены ошибки для компоненты скорости w . Ошибка численного решения Q H по отношению к точным решению Q E измеряется в л ∞ -произошла и непрерывный л 1 и L 2 норм, 31 где интегрирование аппроксимировано интегрированием по Гауссу с удвоенным порядком точности, чем в численной схеме. L ∞ -норма аппроксимируется максимальной ошибкой, возникающей в любой из этих гауссовских точек интегрирования. Порядки сходимости затем вычисляются с помощью 32, где h s указывает шаг сетки h ячейки с номером s в последовательности ячеек. Первый столбец в таблицах 1 и 3 показывает шаг сетки х , представленный максимальным диаметром описанных сфер тетраэдров. В следующих шести столбцах показаны ошибки L ∞ , L 1 и L 2 с соответствующими порядками сходимости, определяемые последовательно сгущающимися сетками.
Ошибка численного решения Q H по отношению к точным решению Q E измеряется в л ∞ -произошла и непрерывный л 1 и L 2 норм, 31 где интегрирование аппроксимировано интегрированием по Гауссу с удвоенным порядком точности, чем в численной схеме. L ∞ -норма аппроксимируется максимальной ошибкой, возникающей в любой из этих гауссовских точек интегрирования. Порядки сходимости затем вычисляются с помощью 32, где h s указывает шаг сетки h ячейки с номером s в последовательности ячеек. Первый столбец в таблицах 1 и 3 показывает шаг сетки х , представленный максимальным диаметром описанных сфер тетраэдров. В следующих шести столбцах показаны ошибки L ∞ , L 1 и L 2 с соответствующими порядками сходимости, определяемые последовательно сгущающимися сетками. В последнем столбце указано время процессора в секундах, необходимое для достижения конечного времени моделирования T = 0,1 с последовательной версией кода на одном процессоре Pentium Xeon с тактовой частотой 3,6 ГГц и 4 ГБ оперативной памяти.
В последнем столбце указано время процессора в секундах, необходимое для достижения конечного времени моделирования T = 0,1 с последовательной версией кода на одном процессоре Pentium Xeon с тактовой частотой 3,6 ГГц и 4 ГБ оперативной памяти.Таблица 1.
Скорости численной сходимости для переменной w с использованием схем ADER-DG с локальным шагом по времени от второго до шестого порядка на неправильных тетраэдрических сетках, показанных на рис. 3.
Таблица 1.
Скорости численной сходимости для переменной w с использованием схем ADER-DG с локальным шагом по времени от второго до шестого порядка на неправильных тетраэдрических сетках, показанных на рис.3.
Таблица 3.
Скорости численной сходимости для переменной w с использованием схем ADER-DG с локальным шагом по времени от второго до шестого порядка на правильных тетраэдрических сетках, включая четыре полоски, как показано на рис. 4.
Таблица 3.
Скорости численной сходимости для переменной w с использованием схем ADER-DG с локальным шагом по времени от второго до шестого порядка на правильных тетраэдрических сетках, включающих четыре полоски, как показано на рис.4.
4.1 Пример 1: Тетраэдрическая сетка с сильно меняющимся размером элемента
Исследование сходимости для определения численного порядка точности сначала выполняется на последовательности неправильных тетраэдрических сеток, как показано на рис. 3, где отношение длин ребер наибольшего тетраэдра к наименьшему выбрано равным ч макс / ч мин = 5.
Рис. 3.
Последовательность неправильных тетраэдральных сеток, использованных для численного анализа сходимости схемы локального шага по времени.
Рис. 3.
Последовательность неправильных тетраэдрических сеток, использованных для численного анализа сходимости схемы локального шага по времени.
Из численных скоростей сходимости, показанных в таблице 1, мы делаем вывод, что предлагаемая нами схема LTS ADER-DG идеально сохраняет точность времени даже при использовании LTS. В то же время схема повышает вычислительную эффективность, поскольку в каждом элементе можно использовать оптимальный шаг по времени. Основным преимуществом такого алгоритма является значительное повышение надежности по отношению к базовой сетке, которая для очень сложных реалистичных трехмерных геометрий может содержать элементы с сильно различающимся размером элементов.Например, в приложениях с топографией поверхности, близкой к поверхности, обычно необходимо использовать довольно мелкую сетку, чтобы правильно разрешить особенности топографии, тогда как в более глубоких областях под поверхностью менее быстро изменяющиеся геометрические особенности могут позволить более крупные. элементы. Для глобальной схемы шага по времени элементы на поверхности ограничивали бы шаг по времени для всех остальных элементов, даже для больших элементов, находящихся далеко под поверхностью.
Чтобы изучить ускорение, вызванное LTS, и, кроме того, для оценки точности p τ -адаптивной версии схемы, мы снова выполняем тот же анализ сходимости, используя схему ADER-DG с глобальным временным шагом четвертого порядка. как представлено в Käser & Dumbser (2006) и Dumbser & Käser (2006) в качестве ссылки.Результаты, показанные в таблице 2, ясно показывают, что алгоритм, представленный в этой статье, с использованием метода LTS намного быстрее, чем алгоритм, использующий глобальное временное пошаговое выполнение. В самой мелкой сетке время ЦП, необходимое для схемы LTS, составляет менее 28 процентов от глобального метода временного шага. Еще одно интересное дополнительное преимущество LTS заключается в том, что метод не только быстрее, но и дает результаты даже в раз лучше . Это происходит из-за равномерно высокого локального числа CFL, которое должно быть как можно больше, чтобы иметь наименьшие ошибки из-за численной диссипации и дисперсии. Используя глобальный шаг по времени, локальное число CFL довольно мало в больших тетраэдрах, что приводит к ненужной численной диссипации и дисперсии. Подробная информация о корреляции количества КЛЛ и ошибок дисперсии и рассеяния схем ADER FV приведена в Dumbser et al. (2006а).
Используя глобальный шаг по времени, локальное число CFL довольно мало в больших тетраэдрах, что приводит к ненужной численной диссипации и дисперсии. Подробная информация о корреляции количества КЛЛ и ошибок дисперсии и рассеяния схем ADER FV приведена в Dumbser et al. (2006а).
Таблица 2.
Сравнение схем ADER-DG, использующих глобальный шаг по времени с чистыми элементами P3 (вверху), локальный шаг по времени с чистыми элементами P3 (в середине) и шаг по локальному времени с элементами P2 и P3 (внизу).Анализируемой переменной является w , сетки, использованные для этого теста, показаны на рис. 3.
чистые элементы P3 (в центре) и пошаговое локальное время с элементами P2 и P3 (внизу). Анализируемой переменной является w , сетки, использованные для этого теста, показаны на рис. 3. эффективность, без потери точности по отношению к схеме LTS ADER-DG с использованием чистых элементов P3 ( N = 3).Однако отметим, что на достаточно мелких сетках глобальный порядок точности смешанной схемы P2-P3 должен снижаться до . В показанном тестовом примере ускорение за счет p τ -адаптивной схемы довольно мало. Это связано с тем, что только небольшое количество элементов использует редуцированный порядок. Однако использование более низкого порядка в малых тетраэдрах внутри сетки выгодно с нескольких точек зрения: во-первых, маленькие тетраэдры приводят к более высокому пространственному разрешению по сравнению с большими тетраэдрами снаружи домена.Следовательно, использование метода более низкого порядка оправдано, чтобы сбалансировать точность во всей сетке. Во-вторых, метод ADER-DG низшего порядка предполагает более щедрый предел устойчивости шага по времени, поскольку для схем DG предел шага по времени зависит не только от максимальной скорости волны и размера элемента, но и от степени N . базисных полиномов. Таким образом, уменьшение порядка в малых тетраэдрах может в какой-то мере компенсировать более жесткое ограничение шага по времени из-за малого размера элементов.В-третьих, элементы более низкого порядка (P2) внутри области вычислительно быстрее, чем элементы более высокого порядка (P3) в остальной части домена.
В показанном тестовом примере ускорение за счет p τ -адаптивной схемы довольно мало. Это связано с тем, что только небольшое количество элементов использует редуцированный порядок. Однако использование более низкого порядка в малых тетраэдрах внутри сетки выгодно с нескольких точек зрения: во-первых, маленькие тетраэдры приводят к более высокому пространственному разрешению по сравнению с большими тетраэдрами снаружи домена.Следовательно, использование метода более низкого порядка оправдано, чтобы сбалансировать точность во всей сетке. Во-вторых, метод ADER-DG низшего порядка предполагает более щедрый предел устойчивости шага по времени, поскольку для схем DG предел шага по времени зависит не только от максимальной скорости волны и размера элемента, но и от степени N . базисных полиномов. Таким образом, уменьшение порядка в малых тетраэдрах может в какой-то мере компенсировать более жесткое ограничение шага по времени из-за малого размера элементов.В-третьих, элементы более низкого порядка (P2) внутри области вычислительно быстрее, чем элементы более высокого порядка (P3) в остальной части домена. Поскольку в алгоритме LTS маленькие элементы должны делать больше шагов по времени, чем большие, это приводит к дополнительному выигрышу в отношении времени ЦП.
Поскольку в алгоритме LTS маленькие элементы должны делать больше шагов по времени, чем большие, это приводит к дополнительному выигрышу в отношении времени ЦП.
4.2 Пример 2: Тетраэдрическая сетка с четырьмя крайне деформированными ленточными элементами
Этот второй набор тестов очень похож на предыдущий. Однако теперь мы рассмотрим последовательность правильных тетраэдрических сеток, в которую введен набор из четырех вырожденных тетраэдров, так называемых щепок, см.4. Четыре осколка были сгенерированы на основе идеально правильной тетраэдрической сетки, делящей координаты z x 3 на 1000 для вершины V = (0/0/ x 3 ) положительная ось z , ближайшая к началу координат O = (0/0/0). После этой модификации модифицированная вершина и начало координат O практически совпадают. Это приводит к четырем крайне вырожденным тетраэдрам, связанным с модифицированной вершиной V ′ и началом координат O так, что их уже невозможно увидеть без сильного увеличения. Их расположение показано стрелками на рис. 4. Из-за жесткого ограничения шага по времени, вызванного такими элементами, представленные сетки не могут быть практически использованы классическими схемами явного шага по времени. Однако, как показано в Таблице 3, предлагаемый нами метод локального шага по времени обеспечивает идеальную скорость сходимости за разумное время ЦП даже на сетке, содержащей такие вырожденные элементы. Запуск схемы на идеально правильной тетраэдрической сетке без модификации дает почти такие же нормы ошибок.
Их расположение показано стрелками на рис. 4. Из-за жесткого ограничения шага по времени, вызванного такими элементами, представленные сетки не могут быть практически использованы классическими схемами явного шага по времени. Однако, как показано в Таблице 3, предлагаемый нами метод локального шага по времени обеспечивает идеальную скорость сходимости за разумное время ЦП даже на сетке, содержащей такие вырожденные элементы. Запуск схемы на идеально правильной тетраэдрической сетке без модификации дает почти такие же нормы ошибок.
Рисунок 4.
Последовательность правильных тетраэдрических сеток, включая набор вырожденных тетраэдров (щепок), указанных между стрелками.
Рис. 4.
Последовательность правильных тетраэдрических сеток, включая набор вырожденных тетраэдров (щепок), указанных между стрелками.
Хотя такое экстремальное соотношение ч макс / ч мин = 1000 может показаться не очень реалистичным, мы добавили этот очень сложный пример, чтобы подчеркнуть возможности и надежность LTS ADER -ДГ метод даже в такой экстремальной ситуации. Реальные приложения, в которых действительно может возникнуть это огромное несоответствие в размерах элементов, могут заключаться в моделировании землетрясений в региональном масштабе, когда интересующие мелкомасштабные объекты, такие как здания или мосты, встраиваются непосредственно в численную модель, используемую для моделирования землетрясений. Такое приложение может представлять интерес в гражданском строительстве, где необходимо изучить воздействие землетрясений на строительные конструкции с целью оценки их безопасности.
Реальные приложения, в которых действительно может возникнуть это огромное несоответствие в размерах элементов, могут заключаться в моделировании землетрясений в региональном масштабе, когда интересующие мелкомасштабные объекты, такие как здания или мосты, встраиваются непосредственно в численную модель, используемую для моделирования землетрясений. Такое приложение может представлять интерес в гражданском строительстве, где необходимо изучить воздействие землетрясений на строительные конструкции с целью оценки их безопасности.
5 Примеры применения
5.1 слой над полупространством
Мы применяем предложенный метод ADER-DG к четко определенной трехмерной тестовой задаче, которая была опубликована в заключительном отчете LIFELINES PROGRAM TASK 1 A 01 (день 2001 г.) Тихоокеанского исследовательского центра землетрясений. . Тестовый пример является частью межведомственного проекта проверки кода ряда различных численных методов, используемых для численного моделирования движения грунта при землетрясении в трехмерных моделях Земли. Помимо квазианалитического решения существуют результаты моделирования из пяти различных хорошо зарекомендовавших себя кодов, которые служат дополнительными эталонными решениями.Результаты этих пяти кодов обозначаются четырехзначными аббревиатурами, указывающими на соответствующие учреждения.
. Тестовый пример является частью межведомственного проекта проверки кода ряда различных численных методов, используемых для численного моделирования движения грунта при землетрясении в трехмерных моделях Земли. Помимо квазианалитического решения существуют результаты моделирования из пяти различных хорошо зарекомендовавших себя кодов, которые служат дополнительными эталонными решениями.Результаты этих пяти кодов обозначаются четырехзначными аббревиатурами, указывающими на соответствующие учреждения.
- (i)
UCBL (Дуг Дрегер и Шон Ларсен, Калифорнийский университет, Беркли/Ливерморская национальная лаборатория).
- (ii)
UCSB (Ким Олсен, Калифорнийский университет, Санта-Барбара).
- (iii)
WCC1 (Robert Graves, URS Corporation).
- (iv)
WCC2 (Арбен Питарка, Корпорация УРС).
- (v)
CMUN (Джакобо Билак, Университет Карнеги-Меллона).
Первые четыре кода используют конечные разности однородных структурированных сеток со смещенным расположением компонент скорости и напряжения и точностью четвертого порядка в пространстве. Однако у нас нет подробной информации об их различиях в том, что касается их конкретной формулировки или реализации. Код CMUN использует кусочно-линейную интерполяцию на неструктурированных тетраэдрических конечных элементах.
Однако у нас нет подробной информации об их различиях в том, что касается их конкретной формулировки или реализации. Код CMUN использует кусочно-линейную интерполяцию на неструктурированных тетраэдрических конечных элементах.
Квазианалитическое решение представляет собой частотно-волновое решение, полученное модификацией метода, представленного в Luco & Apsel (1983) и Apsel & Luco (1983), и сравнивается со всеми численными решениями для оценки их точности.Постановка тестовой задачи LOH.1 подробно описана в Dumbser & Käser (2006). Вещественные параметры слоя (Среда 1) кровли 1000 м и полупространства (Среда 2) приведены в табл. 4.
Таблица 4.
Параметры материала для тестового примера LOH.1.
Таблица 4.
Параметры материала для тестового примера LOH.1.
Сейсмический источник представляет собой точечную дислокацию, представленную источником двойной пары, где единственными ненулевыми элементами тензора сейсмического момента являются = М 0 = 10 18 Н·м. Расположение источника точки ( x S , y S , Z S ) = (0 м, 0 м, 2000 м), то есть в центре плоскости x y области Ω на глубине 2000 м.
Расположение источника точки ( x S , y S , Z S ) = (0 м, 0 м, 2000 м), то есть в центре плоскости x y области Ω на глубине 2000 м.
Расчетная область Ω дискретизируется неструктурированной тетраэдрической сеткой, как показано на рис. 5 с использованием 776 523 элементов. Кроме того, сетка генерируется особым образом для уменьшения паразитных отражений от границ доменов. С этой целью исходная расчетная область Ω = [−15 000 м, 15 000 м]×[−15 000 м, 15 000 м]×[0 м, 17 000 м] дискретизируется элементами с использованием средней длины ребра 350 м на поверхности и 900 м на дне модели. Затем, чтобы уменьшить паразитные отражения от границы, расчетная область встраивается в гораздо большую расширенную область Ω ext = [−50 000 м, 50 000 м]×[−50 000 м, 50 000 м]× [0 м, 25 000 м], который дискретизирован с использованием очень грубых тетраэдров со средней длиной ребра 2000 м.Поскольку большие дополнительные элементы (около 23 % от общего числа элементов) допускают также большие временные шаги, вызванные дополнительные вычислительные затраты весьма малы (примерно на 16 % больше процессорного времени) из-за использования локального временного шага. Заметим, что сетка учитывает границу раздела материалов между Средой 1 и Средой 2, поскольку грани тетраэдрических элементов выровнены с границей материала, как показано на рис.
5 с использованием 776 523 элементов. Кроме того, сетка генерируется особым образом для уменьшения паразитных отражений от границ доменов. С этой целью исходная расчетная область Ω = [−15 000 м, 15 000 м]×[−15 000 м, 15 000 м]×[0 м, 17 000 м] дискретизируется элементами с использованием средней длины ребра 350 м на поверхности и 900 м на дне модели. Затем, чтобы уменьшить паразитные отражения от границы, расчетная область встраивается в гораздо большую расширенную область Ω ext = [−50 000 м, 50 000 м]×[−50 000 м, 50 000 м]× [0 м, 25 000 м], который дискретизирован с использованием очень грубых тетраэдров со средней длиной ребра 2000 м.Поскольку большие дополнительные элементы (около 23 % от общего числа элементов) допускают также большие временные шаги, вызванные дополнительные вычислительные затраты весьма малы (примерно на 16 % больше процессорного времени) из-за использования локального временного шага. Заметим, что сетка учитывает границу раздела материалов между Средой 1 и Средой 2, поскольку грани тетраэдрических элементов выровнены с границей материала, как показано на рис. 5.
5.
Рисунок 5.
Вырезать дискретизацию LOH.1 для визуализации тетраэдрической сетки, которая расширена крупными элементами, чтобы обеспечить лучшее поглощение граничных условий.
Рисунок 5.
Вырежьте дискретизацию модели LOH.1, чтобы визуализировать тетраэдрическую сетку, которая расширена крупными элементами, чтобы обеспечить лучшие поглощающие граничные условия.
Далее мы представляем сравнение наших результатов, полученных с LTS ADER-DG и LTS ADER-DG, и лучших четырех результатов эталонных кодов (UCBL, UCSB, WCC2 и CMUN) с аналитическим решением.Подчеркнем, что максимальная полиномиальная степень базисных функций для ADER-DG составляет N = 3, так что выбранное разрешение сетки для наименьшей средней длины ребра тетраэдра 350 м соответствует требованиям эталонного теста LOH.1, который требовал характерный размер ячеи 100 мкм. Аналогично тестовому сценарию LOH.1 в программе LIFELINES PROGRAM TASK 1 A 01 визуальное сравнение на рис. 6 показывает радиальную, поперечную и вертикальную составляющие поля сейсмической скорости, зарегистрированные приемником 10 в точке ( x ). 10 , y 10 , z 10 ) = (6000 м, 8000 м, 0 м).Кроме того, каждый график дает относительное несоответствие сейсмограммы 34, где n t — количество временных отсчетов сейсмограммы, с j — числовое значение конкретной сейсмограммы на выборке j s a j – соответствующее аналитическое значение. Мы отмечаем, что для всех показанных сейсмограмм исходный источник был деконволюционирован и заменен гауссианой с разбросом 0,05, как описано в Day (2001).
6 показывает радиальную, поперечную и вертикальную составляющие поля сейсмической скорости, зарегистрированные приемником 10 в точке ( x ). 10 , y 10 , z 10 ) = (6000 м, 8000 м, 0 м).Кроме того, каждый график дает относительное несоответствие сейсмограммы 34, где n t — количество временных отсчетов сейсмограммы, с j — числовое значение конкретной сейсмограммы на выборке j s a j – соответствующее аналитическое значение. Мы отмечаем, что для всех показанных сейсмограмм исходный источник был деконволюционирован и заменен гауссианой с разбросом 0,05, как описано в Day (2001).Рисунок 6.
Сравнение компонентов радиальной, поперечной и вертикальной скорости для тестового примера LOH.1 на приемнике 10. Аналитическое решение (жирная линия) нанесено на график относительно численного решения (тонкая линия), полученного с помощью (a) UCBL , (b) UCSB, (c) WCC2, (d) CMUN, (e) LTS ADER-DG и (f) LTS ADER-DG . Относительное несоответствие сейсмограммы E из ур. (34) дается для каждой трассы.
Относительное несоответствие сейсмограммы E из ур. (34) дается для каждой трассы.
Рис. 6.
Сравнение радиальной, поперечной и вертикальной составляющих скорости для LOH.1 тестовый случай на приемнике 10. Аналитическое решение (жирная линия) нанесено на график относительно численного решения (тонкая линия), полученного с помощью (a) UCBL, (b) UCSB, (c) WCC2, (d) CMUN, (e) LTS. ADER-DG и (f) LTS ADER-DG . Относительное несоответствие сейсмограммы E из ур. (34) дается для каждой трассы.
Как показано на рис. 6(a)–(f), все численные решения (тонкая линия) воспроизводят аналитическое решение (толстая линия) с разной степенью невязки. Однако четыре эталонных решения, показанные на рис. 6(a)–(d), вызывают нефизические колебания, возможно, из-за ошибок дисперсии, особенно на поперечной составляющей между 4.5 и 6 с. Эти ошибки значительно уменьшаются схемой LTS ADER-DG четвертого порядка и даже больше схемой LTS ADER-DG. Кроме того, выбросы и фазовые ошибки, полученные всеми эталонными кодами и в основном ответственные за относительное несоответствие сейсмограммы в (34), уменьшаются методами ADER-DG, как показано в 6(e) и (f), что приводит к более точному совпадение численного и аналитического решений. Мы отмечаем, что со схемами ADER-DG, использующими глобальный временной шаг, как представлено в Dumbser & Käser (2006), колебания были видны на сейсмограммах после 6.5 с из-за граничных эффектов. Схемы LTS ADER-DG, представленные в этой статье, могут обрабатывать расширенную вычислительную область Ω ext , показанную на рис. 5, чтобы получить лучшие неотражающие граничные условия без особых дополнительных усилий ЦП, поскольку дополнительная область содержит лишь относительно небольшое число очень больших элементов, которые используют большие временные шаги и, следовательно, добавляют лишь небольшие вычислительные затраты. Сейсмограммы, представленные в этой статье, действительно показывают значительное уменьшение этих колебаний, см. рис. 6(e) и (f).
Мы отмечаем, что со схемами ADER-DG, использующими глобальный временной шаг, как представлено в Dumbser & Käser (2006), колебания были видны на сейсмограммах после 6.5 с из-за граничных эффектов. Схемы LTS ADER-DG, представленные в этой статье, могут обрабатывать расширенную вычислительную область Ω ext , показанную на рис. 5, чтобы получить лучшие неотражающие граничные условия без особых дополнительных усилий ЦП, поскольку дополнительная область содержит лишь относительно небольшое число очень больших элементов, которые используют большие временные шаги и, следовательно, добавляют лишь небольшие вычислительные затраты. Сейсмограммы, представленные в этой статье, действительно показывают значительное уменьшение этих колебаний, см. рис. 6(e) и (f).
Учитывая время ЦП, сравнение оказалось затруднительным, поскольку данные о времени ЦП не были доступны в итоговом отчете о ПРОГРАММНОЙ ЗАДАЧЕ LIFELINES PROGRAM TASK 1 A 01 (день 2001 г.) Pacific Earthquake Engineering Research.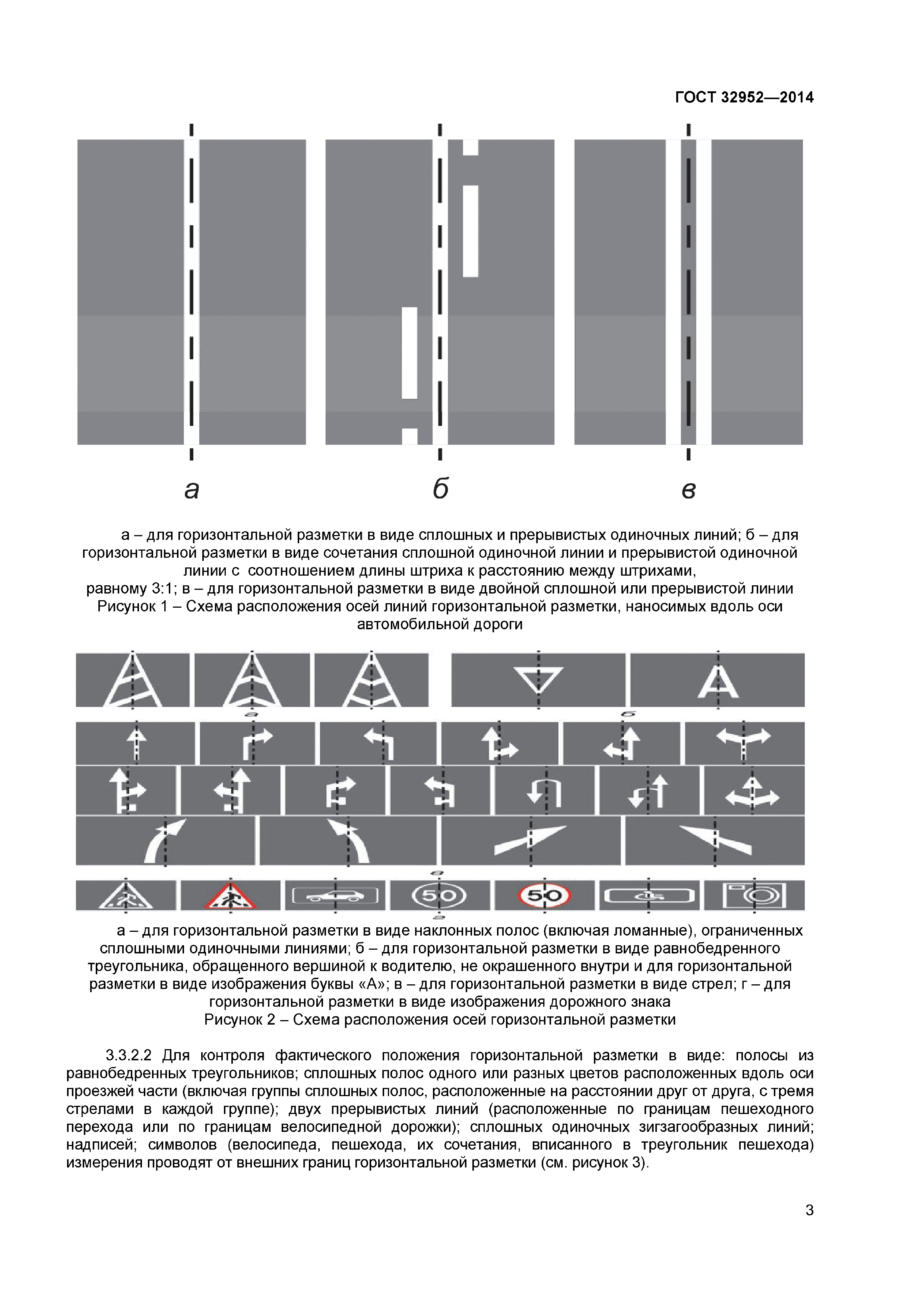 Центр. Более того, все эталонные коды были запущены на разных машинах и с разным уровнем распараллеливания. Тем не менее, чтобы дать точное представление о требованиях к процессорному времени для нашего моделирования LTS ADER-DG: запуск был выполнен на суперкомпьютере HLRB2 Leibniz Rechenzentrum в Мюнхене, Германия, и занял 5.9 часов автономной работы на 128 процессорах Intel Itanium2 Madison 9M, каждый с тактовой частотой 1,6 ГГц и 4,0 ГБ ОЗУ. Для сравнения, те же вычисления с ADER-DG с глобальным временным шагом заняли 12 часов при той же аппаратной конфигурации.
Центр. Более того, все эталонные коды были запущены на разных машинах и с разным уровнем распараллеливания. Тем не менее, чтобы дать точное представление о требованиях к процессорному времени для нашего моделирования LTS ADER-DG: запуск был выполнен на суперкомпьютере HLRB2 Leibniz Rechenzentrum в Мюнхене, Германия, и занял 5.9 часов автономной работы на 128 процессорах Intel Itanium2 Madison 9M, каждый с тактовой частотой 1,6 ГГц и 4,0 ГБ ОЗУ. Для сравнения, те же вычисления с ADER-DG с глобальным временным шагом заняли 12 часов при той же аппаратной конфигурации.
5.2 Жесткое трехмерное включение
После проверки схемы LTS ADER-DG с помощью исследований конвергенции и тестового примера LOH.1 в этом разделе мы рассмотрим трехмерное расширение тестового примера включения, приведенного в LeVeque (2002) и Käser & Dumbser (2006). чтобы показать эффективность и высокую гибкость, обеспечиваемую p τ -адаптивной схемой LTS ADER-DG, на более сложном в геометрическом и вычислительном отношении примере. Расчетная область этого теста состоит из цилиндра радиусом R = 1 и длиной L = 2, в который вложен круговой конус длиной l = 1, радиус дна r 1 = 0,1 и радиус вершины r 2 = 0,001. Оба встроенных тела выровнены по оси z . Свойства материала: λ i = 200 и μ i = 100 внутри встроенного конуса и λ o = 2 и μ o 90Плотность постоянна ρ = 1 везде. Такой выбор параметров материала приводит к десятикратно более высоким скоростям P — и S -волн внутри конусообразного включения, автоматически вызывая гораздо более жесткое ограничение шага по времени, чем во внешнем материале. Кроме того, сетка должна быть сильно измельчена по направлению к вершине конуса, чтобы правильно разрешить геометрию, см. рис. 7, где изображен разрез всей сетки задачи, содержащей 172 836 элементов.Шаг ячеек вне включения h max = 0,045, а на вершине конуса h min = 0,00157, чтобы разрешить вершину конуса с четырьмя ребрами сетки.
Расчетная область этого теста состоит из цилиндра радиусом R = 1 и длиной L = 2, в который вложен круговой конус длиной l = 1, радиус дна r 1 = 0,1 и радиус вершины r 2 = 0,001. Оба встроенных тела выровнены по оси z . Свойства материала: λ i = 200 и μ i = 100 внутри встроенного конуса и λ o = 2 и μ o 90Плотность постоянна ρ = 1 везде. Такой выбор параметров материала приводит к десятикратно более высоким скоростям P — и S -волн внутри конусообразного включения, автоматически вызывая гораздо более жесткое ограничение шага по времени, чем во внешнем материале. Кроме того, сетка должна быть сильно измельчена по направлению к вершине конуса, чтобы правильно разрешить геометрию, см. рис. 7, где изображен разрез всей сетки задачи, содержащей 172 836 элементов.Шаг ячеек вне включения h max = 0,045, а на вершине конуса h min = 0,00157, чтобы разрешить вершину конуса с четырьмя ребрами сетки. Это приводит к соотношению размеров ячеек между наибольшим и наименьшим элементом примерно ч макс. / ч мин = 28,6.
Это приводит к соотношению размеров ячеек между наибольшим и наименьшим элементом примерно ч макс. / ч мин = 28,6.
Рисунок 7.
Тетраэдрическая сетка, используемая для трехмерного теста включения.
Рисунок 7.
Тетраэдрическая сетка, используемая для трехмерного теста включения.
Это уточнение приводит к дополнительному уменьшению шага по времени в вершине конуса по отношению к остальным элементам включения. Использование глобального временного шага и постоянной полиномиальной степени во всей вычислительной области приведет к отношению наименьшего временного шага, возникающего на вершине конуса, к наибольшему временному шагу, возникающему во внешней области, примерно 1:300. Очевидно, что такое большое расхождение во временных шагах приводит к неоправданно высоким вычислительным затратам, особенно для трехмерного приложения.Поскольку в жестком конусообразном включении скорости волн намного выше, чем во внешнем материале, следует ожидать во включении гораздо больших длин волн, чем в остальной части цилиндра. Этот эффект уже был подтвержден в 2D-постановке (см. LeVeque 2002; Käser & Dumbser 2006). Поэтому адекватно использовать приближение более низкого порядка во включении, поскольку для больших длин волн требуется меньшее пространственное разрешение. Преимущества этой аппроксимации более низкого порядка внутри конуса вместе с алгоритмом LTS двояки: во-первых, использование схемы ADER-DG более низкого порядка во включении приводит к большему временному шагу, поскольку временной шаг схем DG уменьшается со степенью базисных полиномов N как 1/(2 N + 1) по уравнению.(9). Во-вторых, используя схему LTS ADER-DG, маленькие тетраэдры во включении будут делать гораздо больше шагов по времени, чем тетраэдры во внешнем материале, поэтому удобно использовать более дешевый метод в той части области, где большая часть циклов ожидаемые. В наших конкретных условиях мы используем метод третьего порядка ( N = 2) внутри включения и метод шестого порядка ( N = 5) в остальной части домена.
Этот эффект уже был подтвержден в 2D-постановке (см. LeVeque 2002; Käser & Dumbser 2006). Поэтому адекватно использовать приближение более низкого порядка во включении, поскольку для больших длин волн требуется меньшее пространственное разрешение. Преимущества этой аппроксимации более низкого порядка внутри конуса вместе с алгоритмом LTS двояки: во-первых, использование схемы ADER-DG более низкого порядка во включении приводит к большему временному шагу, поскольку временной шаг схем DG уменьшается со степенью базисных полиномов N как 1/(2 N + 1) по уравнению.(9). Во-вторых, используя схему LTS ADER-DG, маленькие тетраэдры во включении будут делать гораздо больше шагов по времени, чем тетраэдры во внешнем материале, поэтому удобно использовать более дешевый метод в той части области, где большая часть циклов ожидаемые. В наших конкретных условиях мы используем метод третьего порядка ( N = 2) внутри включения и метод шестого порядка ( N = 5) в остальной части домена. Начальное условие задается плоской гауссовой P -волной, движущейся в положительном направлении z : 35 Здесь вектор нормали равен , начальное положение центра гауссовского распределения равно x 0 = 0.25 полуширина выбрана равной σ = 0,03 и является собственным вектором, связанным с соответствующей волной P . Это приводит к среднему разрешению падающей плоской волны 2σ/ ч max = 1,3 элемента. Мы вычисляем задачу до t = 0,3. Время настенных часов, необходимое для адаптивной схемы LTS ADER-DG p τ на суперкомпьютере HLRB2 LRZ в Мюнхене, Германия, составляло 57 часов с использованием 128 процессоров Intel Itanium 2 Madison, каждый с 1.6 ГГц и 4 ГБ оперативной памяти. Общее количество обновлений элементов, необходимых для достижения этого времени вывода с использованием различных схем ADER-DG, следующее.
Начальное условие задается плоской гауссовой P -волной, движущейся в положительном направлении z : 35 Здесь вектор нормали равен , начальное положение центра гауссовского распределения равно x 0 = 0.25 полуширина выбрана равной σ = 0,03 и является собственным вектором, связанным с соответствующей волной P . Это приводит к среднему разрешению падающей плоской волны 2σ/ ч max = 1,3 элемента. Мы вычисляем задачу до t = 0,3. Время настенных часов, необходимое для адаптивной схемы LTS ADER-DG p τ на суперкомпьютере HLRB2 LRZ в Мюнхене, Германия, составляло 57 часов с использованием 128 процессоров Intel Itanium 2 Madison, каждый с 1.6 ГГц и 4 ГБ оперативной памяти. Общее количество обновлений элементов, необходимых для достижения этого времени вывода с использованием различных схем ADER-DG, следующее.- (i)
71,665 × 10 9 с использованием схемы ADER-DG чисто шестого порядка ( N = 5) с глобальным временным шагом.

- (ii)
32,575 × 10 9 с использованием p τ — адаптивная схема ADER-DG ( N = 2 и 5) с глобальным временем
- (iii)
954.47 × 10 6 с использованием схемы ADER-DG чисто шестого порядка ( N = 5) с локальным шагом по времени.
- (iv)
573,84 × 10 6 с использованием p τ -адаптивной схемы ADER-DG ( N = 2 и 5) с местным временем
Это приводит к сокращению времени процессора более чем в 125 раз для p τ -адаптивного метода LTS ADER-DG по сравнению с использованием схемы ADER-DG шестого порядка с глобальным временным шагом везде, учитывая только количество обновлений элементов.Дальнейшая экономия ЦП для адаптивной схемы p τ обусловлена тем, что элементы третьего порядка дешевле элементов шестого порядка.
На рис. 8 показан разрез расчетной области в плоскости x − z при y = 0 для времени t = 0,3. Изображена составляющая напряжения σ zz , полученная с помощью p τ -адаптивной схемы LTS ADER-DG. Подобно двумерным результатам, показанным в LeVeque (2002) и Käser & Dumbser (2006), мы можем видеть прямую волну P , волны Рэлея на внешней поверхности цилиндра и поперечные волны, возникающие из включения из-за отражения волны P внутри конуса из-за большой разницы свойств материалов.
Изображена составляющая напряжения σ zz , полученная с помощью p τ -адаптивной схемы LTS ADER-DG. Подобно двумерным результатам, показанным в LeVeque (2002) и Käser & Dumbser (2006), мы можем видеть прямую волну P , волны Рэлея на внешней поверхности цилиндра и поперечные волны, возникающие из включения из-за отражения волны P внутри конуса из-за большой разницы свойств материалов.
Рис. 8.
Компонент напряжения σ zz at t = 0,3, полученный с помощью p τ -адаптивной схемы LTS ADER-DG с использованием элементов P2 и P5.
Рис. 8.
Компонент напряжения σ zz at t = 0,3, полученный по p τ -адаптивной схеме LTS ADER-DG с использованием элементов P2 и P5.
Мы убеждены, что этот тестовый пример является очень сложным для всех явных численных методов, которые должны подчиняться глобальному ограничению шага по времени. Подчеркнем также, что уже создание сетки для этого тестового примера с использованием методов, основанных на шестигранных сетках, не является тривиальной задачей. Сопоставление внутренней сетки внутри конуса с внешней сеткой цилиндра может стать трудным для структурированных и неструктурированных шестигранных сеток, даже при использовании современных коммерческих генераторов сетки.
Подчеркнем также, что уже создание сетки для этого тестового примера с использованием методов, основанных на шестигранных сетках, не является тривиальной задачей. Сопоставление внутренней сетки внутри конуса с внешней сеткой цилиндра может стать трудным для структурированных и неструктурированных шестигранных сеток, даже при использовании современных коммерческих генераторов сетки.
5.3 Моделирование землетрясений и прогноз движения грунта
В этом разделе мы применяем предложенную схему ADER-DG с LTS для эталонного теста моделирования землетрясений, чтобы подтвердить производительность и функциональность этого подхода для реальных приложений.Таким образом, мы выбрали тест ESG 2006 для моделирования движения грунта в долине Гренобля, где подробности приведены в Chaljub (2006). Хорошо известно, что альпийские долины производят сильные эффекты местности из-за контакта и больших контрастов импеданса между твердой коренной породой и менее консолидированными отложениями, как показано в Bard & Buchon (1980a,b). Кроме того, в альпийских долинах обычно наблюдаются сильные топографические вариации свободной поверхности и внутренней границы между коренной породой и осадочным бассейном.
Кроме того, в альпийских долинах обычно наблюдаются сильные топографические вариации свободной поверхности и внутренней границы между коренной породой и осадочным бассейном.
Настройка этого тестового примера обеспечивает скоростную модель горизонтальной протяженности 50,4 × 47,4 км и глубины 35 км, как показано на рис. 9 (a) и (b). Подробная топографическая информация предоставляется цифровой моделью рельефа с разрешением по горизонтали 50 м. Для дискретизации расчетной области используется неструктурированная тетраэдрическая сетка из 1 259 721 элемента, см. рис. 9(а), учитывающая топографию свободной поверхности и внутренние материальные границы, в частности, геометрически сложный интерфейс между осадочным бассейном и коренной материал.Кроме того, сетка локально измельчается в интересующих зонах и укрупняется с увеличением глубины и по направлению к границам модели, как показано на рис. 9 (а). Осадочный бассейн под Греноблем выглядит как структура в форме Y на поверхности, как показано на рис. 9(b). Цветовой код на рис. 9(b) отображает распределение скоростей P волн. Подробная информация о скоростной модели коренных пород приведена в Таблице 5. Параметры материала внутри слоя коренных пород изменяются линейно с глубиной.
9(b). Цветовой код на рис. 9(b) отображает распределение скоростей P волн. Подробная информация о скоростной модели коренных пород приведена в Таблице 5. Параметры материала внутри слоя коренных пород изменяются линейно с глубиной.
Рис. 9.
Визуализация тетраэдрической сетки и ее разбиения на 64 подобласти для эталона долины Гренобля с топографией (а). Топография и скоростная структура модели (б). Увеличенное изображение границы раздела осадок/коренная порода и ее тетраэдризация в разобранном виде (в). Вид рельефа дна осадочного бассейна снизу (г). Расчетная пиковая скорость грунта в долине Гренобля для модели без топографии (д) и с топографией (е).
Рис. 9.
Визуализация тетраэдрической сетки и ее разбиения на 64 подобласти для эталона долины Гренобля с топографией (а). Топография и скоростная структура модели (б). Увеличенное изображение границы раздела осадок/коренная порода и ее тетраэдризация в разобранном виде (в). Вид рельефа дна осадочного бассейна снизу (г). Расчетная пиковая скорость грунта в долине Гренобля для модели без топографии (д) и с топографией (е).
Расчетная пиковая скорость грунта в долине Гренобля для модели без топографии (д) и с топографией (е).
Таблица 5.
Вещественные параметры коренных пород эталона долины Гренобля.
Таблица 5.
Материальные параметры скальной породы эталона долины Гренобля.
Увеличенная иллюстрация трехмерной формы осадочного бассейна и ее дискретизации неструктурированной тетраэдрической сеткой показана на рис. 9(c). Обратите внимание, что на этом графике мы показываем изображение в разобранном виде, так что осадок отделяется от коренной породы, чтобы увидеть внутреннюю границу между двумя геологическими зонами.Распределение вещественных параметров внутри осадочного бассейна по глубине приведено в табл. 6, где единицей глубины d является (м), одной из скоростей c p и c с (мс -1 ) и плотностью ρ (кг м -3 ).
Таблица 6.
Материальные параметры осадочного бассейна репера долины Гренобля.
Таблица 6.
Материальные параметры осадочного бассейна репера Гренобльской долины.
На рис. 9(d) представлен вид снизу осадочного бассейна, чтобы более подробно показать топографию границы раздела отложений и коренных пород вместе с разрезом, чтобы лучше визуализировать тетраэдрические элементы дискретизации бассейна. Отметим, что тетраэдрические элементы, дискретизирующие бассейн, имеют среднюю длину ребра тетраэдра 200 м. В сравнении с тетраэдрическими элементами на глубине 35 км со средней длиной ребра до 6200 м, см.9(а), отношение локального шага сетки дает коэффициент 31. Отметим, что глобальная схема шага по времени должна обновлять эти большие тетраэдры много раз в соответствии с минимальным шагом по времени, который происходит во всей вычислительной области. Однако наша схема LTS использует максимальный временной шаг, допустимый для этих больших тетраэдрических элементов. Отметим, что этот максимальный временной шаг также учитывает локальные материальные параметры, то есть локальные скорости сейсмических волн, и степень локального полинома N полинома аппроксимации. Таким образом, вычислительные усилия могут быть значительно сокращены.
Таким образом, вычислительные усилия могут быть значительно сокращены.
Поскольку сейсмическое затухание должно учитываться внутри структуры бассейна, характеристики затухания аппроксимируются вязкоупругим материалом с использованием трех механизмов затухания в полосе частот от 0,1 до 10 Гц, как это было введено Emmerich & Korn (1987) и подробно описано в структура схем ADER-DG в Käser et al. (2007 г.).
В нашем моделировании мы рассматриваем случай сильного движения, когда параметры протяженного очага разрыва описывают правосторонний сдвиг с магнитудой момента M w = 6.0 в восточной части пограничного разлома Белледон, как указано в Chaljub (2006). Кинематика разрыва представлена круговой трещиной, распространяющейся внутри прямоугольного разлома, т. е. трещиной Хаскелла с постоянным конечным смещением, со скоростью разрыва 2,8 км с -1 . Точка зарождения находится на глубине 3 км и в центре вертикальной плоскости разлома длиной 9 км и шириной 4,5 км с ориентацией: простирание = 45°, падение = 90° и угол наклона = 180°. Плоскость разрыва расчленена на 15 × 30 = 450 субразломов размером 300 × 300 м.Источник реализуется через тензор сейсмического момента, описывающий источник двойной пары с функцией времени источника от скорости смещения 36 с коэффициентом гладкости T = 3,5842 и временем задержки t D = 2,232 с, как описано в Chaljub (2006). Карта расположения приемников на свободной поверхности модели и проекция плоскости разрыва на поверхность с учетом формы и положения осадочного бассейна представлены на рис. 10.
Плоскость разрыва расчленена на 15 × 30 = 450 субразломов размером 300 × 300 м.Источник реализуется через тензор сейсмического момента, описывающий источник двойной пары с функцией времени источника от скорости смещения 36 с коэффициентом гладкости T = 3,5842 и временем задержки t D = 2,232 с, как описано в Chaljub (2006). Карта расположения приемников на свободной поверхности модели и проекция плоскости разрыва на поверхность с учетом формы и положения осадочного бассейна представлены на рис. 10.Рис. 10.
Пространственное расположение и нумерация приемников для реперной задачи долины Гренобля. Показаны также проекция латерального простирания осадочного бассейна (тонкая сплошная линия) и плоскости разрыва (жирная сплошная линия).
Рис. 10.
Пространственное расположение и нумерация приемников для реперной задачи Гренобльской долины. Показаны также проекция латерального простирания осадочного бассейна (тонкая сплошная линия) и плоскости разрыва (жирная сплошная линия).
Для моделирования мы разбиваем модель на четыре геометрические геологические зоны: (1) строение бассейна, (2) поверхностный слой выше глубины 3 км, исключая бассейн, (3) слой между глубиной 3 и 27 км и 4) слой от 27 до 35 км. Используем схему LTS ADER-DG с p τ -адаптивностью, где применяется следующее распределение степени полинома N : зона (1) N = 3, зона (2) 3 ≤ N ≤ 4, зона (3) 3 ≤ N ≤ 4 и зона (4) N = 2.Сетка разделена на 255 подобластей для параллельных вычислений, как показано на рис. 9(а). Общее время моделирования установлено равным 30 с.
В соответствии с эталоном, предложенным Chaljub (2006), расчет сначала выполняется без топографии поверхности, но с учетом структуры бассейна. Эта модель в дальнейшем также обозначается как плоская модель. Во второй расчет также включена сложная топография поверхности. Эти два расчета позволяют оценить влияние топографии поверхности на сейсмограммы и наблюдаемую пиковую скорость грунта.
На рис. 9(д) и (е) представлены карты пиковой скорости грунта, зарегистрированные массивом приемников 120 × 120 с пространственным интервалом 250 м на поверхности по площади долины Гренобля для плоской тестовый пример и модель с топографией поверхности. Наибольшая скорость грунта прогнозируется для юго-восточной части долины Гренобля на контакте между мягкими отложениями и твердой коренной породой, что согласуется с наблюдаемыми эффектами усиления осадочных бассейнов в Chaljub et al. (2005 г.). Хорошо известный фокусирующий эффект волн вдоль направления простирания разрывного разлома может быть отчетливо виден, поскольку область контакта отложений и коренных пород, расположенная ближе, но перпендикулярно плоскости разрыва, демонстрирует скорость грунта гораздо меньшей амплитуды. Кроме того, осадочный бассейн выступает в роли щита, приводящего к относительно слабым движениям грунта на противоположной (западной) стороне долины.
Сравнивая рис. 9(e) и (f), можно ясно увидеть, что для рассматриваемого сейсмического события топография поверхности не оказывает большого влияния на пиковое движение грунта, поскольку наблюдаемые максимальные амплитуды более или менее одинаковы в обоих случаях.
На рисунках 11 и 12 показаны сейсмограммы без масштабирования и нефильтрованные сейсмограммы для трех компонентов скорости в направлениях x , y и z , записанных в 15 положениях приемника, показанных на 15 приемниках, показанных на рис. модель и модель с топографией поверхности. Отметим, что в обоих случаях приемники 4, 32, 33, 38 и 39 показывают гораздо меньшие амплитуды скоростей, чем остальные приемники, поскольку они расположены на коренных породах вне бассейна. Кроме усиления амплитуды сигналы, зарегистрированные в бассейне, имеют большую длительность колебаний из-за многократных отражений волн, захваченных внутри бассейна.Эти эффекты хорошо коррелируют с другими моделями и наблюдениями в этой области, как показано в Chaljub et al. (2005 г.). В соответствии с картами пиковых скоростей грунта, обсуждавшимися ранее, мы наблюдаем путем сравнения данных сейсмограммы для плоской модели и модели топографии поверхности в выбранных местоположениях приемников, что для этого тестового примера имеются лишь небольшие изменения в сейсмограммах из-за эффектов топографии поверхности.
Рисунок 11.
Сейсмограммы, полученные с помощью p τ -адаптивного метода LTS ADER-DG в сравнении с эталонным решением SEM Chaljub et al., показывающий три компонента скорости на 15 выбранных приемниках плоской модели для эталонной задачи Гренобльской долины.
Рисунок 11.
Сейсмограммы, полученные с помощью p τ -адаптивного метода LTS ADER-DG в сравнении с эталонным решением SEM Chaljub et al. , показывающий три компонента скорости на 15 выбранных приемниках плоской модели для эталонной задачи Гренобльской долины.
Рисунок 12.
Сейсмограммы, полученные с помощью p τ -адаптивного метода LTS ADER-DG в сравнении с эталонным решением SEM Chaljub et al. , показывающий три компонента скорости на 15 выбранных приемниках модели с топографией поверхности для эталонной задачи долины Гренобля.
Рисунок 12.
Сейсмограммы, полученные с помощью p τ -адаптивного метода LTS ADER-DG в сравнении с эталонным решением SEM Chaljub et al. , показывающий три компонента скорости на 15 выбранных приемниках модели с топографией поверхности для эталонной задачи долины Гренобля.
, показывающий три компонента скорости на 15 выбранных приемниках модели с топографией поверхности для эталонной задачи долины Гренобля.
Для справки: данные сейсмограммы без масштабирования и нефильтрованной сейсмограммы , полученные Э. Чалюбом с использованием метода SEM для обеих моделей, также нанесены на график для всех рассматриваемых местоположений приемников. В обоих случаях мы отмечаем в целом очень хорошее совпадение между эталонными сейсмограммами SEM и нашими моделями LTS ADER-DG.Не только в отношении амплитуд и фаз, но даже отдельные формы сигналов очень похожи во всех местах расположения приемника. Учитывая геометрическую сложность этого тестового примера с нетривиальным источником, такой высокий уровень согласия между двумя совершенно разными численными методами, работающими на совершенно разных топологиях сетки и настройках модели, как показано в таблице 7, является очень удовлетворительным для обоих методов и подчеркивает надежность современных инструментов численного моделирования в сложных геофизических случаях применения, имеющих практическое значение.
Таблица 7.
Таблица 7.
6 Заключительные замечания
Мы представили произвольную РГ-схему высокого порядка на неструктурированных тетраэдральных сетках, которая может адаптировать локальную полиномиальную степень, а также локальный временной шаг в зависимости от задачи. Очевидным основным преимуществом предложенной схемы LTS ADER-DG является ее исключительная гибкость, учитывая ее способность работать со сложной геометрией, поскольку она может работать на тетраэдрических сетках, а также адаптивность лежащего в основе численного алгоритма.
Поскольку наш численный метод основан на совершенно другой топологии сетки по сравнению с другими методами, такими как FD или SEM, прямое и справедливое сравнение вычислительных затрат очень сложно. Особо отметим, что для создания сетки двух равных расчетных областей с одинаковым шагом сетки, то есть с одинаковой длиной ребер элементов, требуется примерно в шесть раз больше тетраэдрических элементов по сравнению с шестигранной сеткой. В то же время тетраэдры требуют более жесткого ограничения шага по времени (от двух до трех меньших шагов по времени) по сравнению с обычной шестигранной сеткой.Следовательно, чистая вычислительная стоимость нашего метода в целом составляет 90 041 из-за лежащей в основе топологии тетраэдрической сетки. Даже LTS-версия нашей схемы ADER-DG по-прежнему медленнее по сравнению со стандартными методами FD или SEM.
В то же время тетраэдры требуют более жесткого ограничения шага по времени (от двух до трех меньших шагов по времени) по сравнению с обычной шестигранной сеткой.Следовательно, чистая вычислительная стоимость нашего метода в целом составляет 90 041 из-за лежащей в основе топологии тетраэдрической сетки. Даже LTS-версия нашей схемы ADER-DG по-прежнему медленнее по сравнению со стандартными методами FD или SEM.
Тем не менее, мы подчеркиваем, что генерация тетраэдрической сетки почти полностью автоматическая, даже для очень сложных геометрических форм, что определенно дает преимущество гибкости
нашего метода. Все тестовые случаи, представленные в этой статье, были рассчитаны с использованием одного и того же кода, где модель может быть почти полностью настроена уже в генераторе тетраэдральной сетки.Мы используем программный пакет GAMBIT, доступный в суперкомпьютерном центре HLRS в Штутгарте, который позволяет определять так называемые объемные зоны. Для каждой зоны определяются локальные свойства материала (λ, μ, ρ, а также Q p и Q s для вязкоупругого материала), а также степень искомого локального полинома N основных функций. Также граничные условия (свободная поверхность, периодические или открытые границы) могут быть заданы непосредственно в генераторе сетки.Вся генерация тетраэдрической сетки для тестового примера включения, показанного на рис. 7, для схемы LTS ADER-DG может быть выполнена полностью автоматически примерно за 15 с на стандартной рабочей станции Intel Xeon с тактовой частотой 3,6 ГГц и 4 ГБ ОЗУ. Для создания всей трехмерной модели и тетраэдрической сетки для тестового примера долины Гренобля, включая топографию поверхности, как показано на рис. 9(а), генератору сетки GAMBIT потребовалось всего 165 с без каких-либо ручных операций. В отличие от этого, создание шестигранных сеток, как показано в Stupazzini (2006) для того же теста, требует много ручного взаимодействия, и поэтому процесс создания таких шестигранных сеток может легко занять несколько часов даже для опытных пользователей.Принимая во внимание также время, необходимое для создания сетки, схема LTS ADER-DG кажется очень гибкой и практичной альтернативой существующим подходам, таким как схемы FD и SE, которые требуют более трудоемкого создания шестигранной сетки.
Также граничные условия (свободная поверхность, периодические или открытые границы) могут быть заданы непосредственно в генераторе сетки.Вся генерация тетраэдрической сетки для тестового примера включения, показанного на рис. 7, для схемы LTS ADER-DG может быть выполнена полностью автоматически примерно за 15 с на стандартной рабочей станции Intel Xeon с тактовой частотой 3,6 ГГц и 4 ГБ ОЗУ. Для создания всей трехмерной модели и тетраэдрической сетки для тестового примера долины Гренобля, включая топографию поверхности, как показано на рис. 9(а), генератору сетки GAMBIT потребовалось всего 165 с без каких-либо ручных операций. В отличие от этого, создание шестигранных сеток, как показано в Stupazzini (2006) для того же теста, требует много ручного взаимодействия, и поэтому процесс создания таких шестигранных сеток может легко занять несколько часов даже для опытных пользователей.Принимая во внимание также время, необходимое для создания сетки, схема LTS ADER-DG кажется очень гибкой и практичной альтернативой существующим подходам, таким как схемы FD и SE, которые требуют более трудоемкого создания шестигранной сетки. Если вычислительная модель содержит очень сложную геометрию, которую трудно связать с шестигранными сетками, и если вычислительная модель приводит к очень разным временным шагам, таким как представленный эталон долины Гренобля, схема LTS ADER-DG может иметь преимущества благодаря своей гибкости. .В других случаях, например, при моделировании землетрясений в глобальном масштабе, когда основной геометрией является сфера, РЭМ представляется более предпочтительным.
Если вычислительная модель содержит очень сложную геометрию, которую трудно связать с шестигранными сетками, и если вычислительная модель приводит к очень разным временным шагам, таким как представленный эталон долины Гренобля, схема LTS ADER-DG может иметь преимущества благодаря своей гибкости. .В других случаях, например, при моделировании землетрясений в глобальном масштабе, когда основной геометрией является сфера, РЭМ представляется более предпочтительным. Кроме того, предлагаемая схема LTS ADER-DG очень надежна в отношении качества сетки. Как видно из исследований сходимости, представленных в разделе 4, нормы ошибок и процессорное время сравнимы как для нерегулярной сетки, содержащей тетраэдры самого разного размера, так и для регулярной сетки, содержащей четыре осколка. Эта надежность требуется для приложений со сложной геометрией, в которых раздражающая проблема осколков (Джо, 1995; Берн и Эппштейн, 1992; Флейшманн, и др. 1999) может возникнуть во время создания сетки. Такие осколки, если их нельзя избежать, не только снижают качество решения, но и значительно уменьшают временной шаг глобальных схем временного шага, что добавляет ненужное количество процессорного времени.
Такие осколки, если их нельзя избежать, не только снижают качество решения, но и значительно уменьшают временной шаг глобальных схем временного шага, что добавляет ненужное количество процессорного времени.
По нашему мнению, будущим основным применением алгоритма LTS, предложенного в этой статье, могло бы быть встраивание небольших локальных структур, представляющих интерес для гражданского строительства, таких как мосты, башни или другие здания, в сценарий землетрясения в региональном масштабе, где расчетная модель может быть значительно обогащена в пределах интересующей области, например, с учетом структуры подповерхностных отложений и топографии поверхности.Поскольку небольшая уточненная локальная интересующая область не приводит к вырождению временного шага, используемого в глобальном масштабе, глобальное и локальное волновые поля могут быть вычислены одновременно и полностью связанным образом. Вторым важным приложением может быть расчет упругих волн в сложных слоистых структурах отложений, где отложения имеют очень разные свойства материала и, таким образом, вызывают очень разные временные шаги. Третье будущее приложение может относиться к динамическим процессам разрыва, где динамический расчет разрыва может быть выполнен на локально сильно измельченной сетке, требующей очень малых локальных временных шагов.Это динамическое вычисление разрыва затем может быть напрямую связано с вычислением распространения волны в дальнем поле на гораздо более грубой сетке, используя все преимущества допустимых больших временных шагов для вычисления дальнего поля.
Третье будущее приложение может относиться к динамическим процессам разрыва, где динамический расчет разрыва может быть выполнен на локально сильно измельченной сетке, требующей очень малых локальных временных шагов.Это динамическое вычисление разрыва затем может быть напрямую связано с вычислением распространения волны в дальнем поле на гораздо более грубой сетке, используя все преимущества допустимых больших временных шагов для вычисления дальнего поля.
Благодарности
Авторы благодарят Deutsche Forschungsgemeinschaft (DFG), поскольку работа финансировалась DFG Forschungsstipendium (DU 1107/1-1), исследовательской группой DFG-CNRS FOR 508 и Emmy Noether Programm (KA 2281/1-1).
Мы высоко ценим поддержку и комментарии Стивена Дэя по настройке тестового примера LOH.1 и предоставлению аналитических и эталонных решений. Авторы особенно благодарны Э. Чалюбу за тщательную постановку эталонной задачи Гренобльской долины и за предоставление всех необходимых параметров моделирования, а также за численное эталонное решение.
Большое спасибо Leibniz Rechenzentrum в Мюнхене, Германия, и суперкомпьютерному центру HLRS в Штутгарте за предоставление генератора сетки GAMBIT и необходимого оборудования для запуска сложных трехмерных тестов.
Наконец, мы хотели бы поблагодарить двух рецензентов этой статьи, чьи конструктивные комментарии и предложения определенно помогли улучшить ясность и качество этой статьи.
Ссылки
,
2002
.Количественная сейсмология
,University Science Books, Саусалито, Калифорния, США
.,
1983
.О функциях Грина для слоистого полупространства, часть II
,Бюлл.сейсм. соц. Являюсь.
,73
,931
–951
.,
1980а
.Сейсмический отклик долин, заполненных наносами, Часть 1: Случай падающих SH-волн
,Бюлл. сейсм. соц. Являюсь.
,70
,1263
–1286
.,
1980b
.
Сейсмический отклик долин, заполненных наносами, Часть 2: Случай падающих волн P и SV
,Бюлл.сейсм. соц. Являюсь.
,70
,1921
–1941
.,
1994
.Распространение упругих волн
,John Wiley & Sons, Чичестер, Великобритания
.,
1992
.Генерация сетки и оптимальная триангуляция
, inComputing in Euclidean Geometry
, стр.201
–204
, World Scientific,Сингапур
.,
1987
.Численный анализ обыкновенных дифференциальных уравнений: Рунге-Кутта и общие линейные методы
,John Wiley & Sons
,Нью-Йорк
.,
2005
.Спектрально-элементное моделирование распространения трехмерных волн в альпийской долине Гренобля, Франция, в Geophysical Research Abstracts
, Vol. 7, стр.05 225
, 2-я Генеральная ассамблея EGU, Вена, Австрия.,
2006
.Численный контрольный показатель трехмерного моделирования движения грунта в долине Гренобля, Французские Альпы
,.
,
2000
.Щепочный экссудат
,J. ACM 47
,5
,883
–904
.,
2000
.Разрывные методы Галеркина, теория, вычисления и приложения
,LNCSE
, Vol. 11,Спрингер
,Берлин, Германия
.,
2001
.Тесты кодов 3D эластодинамики, ПРОГРАММА LIFELINES PROGRAM TASK 1A01
Заключительный отчет для Тихоокеанского научно-исследовательского центра землетрясений
, 10 сентября 2001 г. Координатор: С.М. Дэй,Государственный университет Сан-Диего
.,
2006
.Произвольный разрывной метод Галеркина высокого порядка для упругих волн на неструктурированных сетках — IV. Анизотропия
.Геофиз. Дж.Междунар.
, в печати.,
2005
.Произвольные схемы высокого порядка для решения гиперболических законов сохранения в сложных областях
,Shaker Verlag
,Ахен
.
,
2005
.Произвольные разрывные схемы Галеркина высокого порядка
, inЧисленные методы решения гиперболических и кинетических задач
, стр.295
–333
, ред. ,Серия ИРМА по математике и теоретической физике, Издательство ЭМС
.,
2006
.Произвольный разрывной метод Галеркина высокого порядка для упругих волн на неструктурированных сетках — II. Трехмерный изотропный случай
.Геофиз. Дж. Междунар.
,167
,316
–336
.,
2006а
.Схемы произвольного конечного объема высокого порядка для линейного распространения волн
, inВычислительные науки и высокопроизводительные вычисления II
, стр.129
–144
, ред. , Заметки о численной гидромеханике и междисциплинарном проектировании (NNFM),Springer
,Берлин/Гейдельберг
.,
2006b
.Произвольные схемы конечных объемов высокого порядка для распространения сейсмических волн на неструктурированных сетках в 2D и 3D
, в печати.
,
2002
.Экспериментальное исследование выделения щепок
,англ.вычисл.
,18
,229
–240
.,
1987
. .,
2004
.Обобщенная схема локального временного шага для эффективного моделирования FVTD в сильно неоднородных сетках
,IEEE Trans.Теория микроволнового излучения.
,52
(3
),1067
–1076
.,
1997
.Адаптивное локальное уточнение с балансировкой нагрузки октодерева для параллельного решения трехмерных законов сохранения
,J. Parallel Distrib. вычисл.
,47
,139
–152
.,
1999
.Генерация сетки для применения в технологии САПР
,IEICE Trans.Электрон.
,E82-C
(6
),937
–947
.,
1995
.Построение трехмерных триангуляций улучшенного качества с использованием локальных преобразований
, SIAM: J. Sci. вычисл.
Sci. вычисл.
16
(6
),1292
–1307
.,
1998
.Многоуровневая схема разбиения k-way для нерегулярных графов
,J. Parallel Distrib.вычисл.
,48
(1
),96
–129
.,
2006
.Произвольный разрывной метод Галеркина высокого порядка для упругих волн на неструктурированных сетках — I. Двумерный изотропный случай с внешними источниками
.Геофиз. Дж. Междунар.
,166
,855
–877
.,
2007
.Произвольный разрывной метод Галеркина высокого порядка для упругих волн на неструктурированных сетках — III.Вязкоупругое затухание
.Геофиз. Дж. Междунар.
,168
,224
–242
.,
1999
.Введение в метод спектральных элементов для распространения трехмерных сейсмических волн
,Геофиз. Дж. Междунар.
,139
,806
–822
.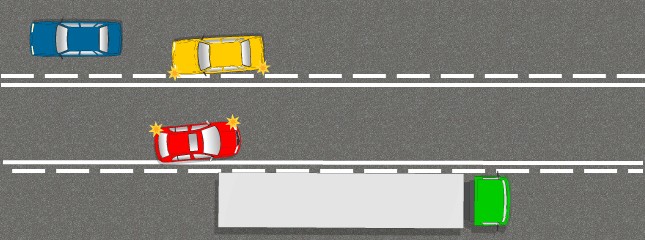
,
2002
.Спектрально-элементное моделирование глобального распространения сейсмических волн — I. Валидация
,Геофиз.Дж. Междунар.
,149
,390
–412
.,
2003
.Идеально согласованное граничное условие поглощающего слоя для сейсмического волнового уравнения второго порядка
,Геофиз. Дж. Междунар.
,154
,146
–153
.,
1998
.Метод спектральных элементов: эффективный инструмент для моделирования сейсмического отклика 2D и 3D геологических структур
,Bull.сейсм. соц. Являюсь.
,88
,368
–392
.,
2002
.Методы конечных объемов для гиперболических задач
,Издательство Кембриджского университета
,Кембридж
.,
2007
.Разрывная схема Галеркина, основанная на пространственно-временном разложении. I. Течение невязкой сжимаемой жидкости в одном пространственном измерении
.
J. Sci. вычисл.
, в печати.,
1983
.О функциях Грина для слоистого полупространства, Часть I
,Бюлл. сейсм. соц. Являюсь.
,73
,909
–929
.,
2006
.3D-моделирование движения грунта в долине Гренобля от GeoELSE, по материалам
3-й Международный симпозиум по влиянию геологии поверхности на сейсмические движения (ESG), Гренобль, Франция.
,
2001
.hp-Адаптивный разрывный метод конечных элементов Галеркина для гиперболических задач первого порядка
,SIAM J.науч. вычисл.
,23
(4
),1225
–1251
.,
2002
.ADER: Годуновский подход произвольного высокого порядка
,J. Sci. вычисл.
,17
,609
–618
.,
2001
.К схемам Годунова очень высокого порядка
, вМетоды Годунова; Теория и приложения
, стр.
907
–940
,Kluwer Academic Plenum Publishers
,Оксфорд
.,
2002
.Решение обобщенной задачи Римана для уравнений переноса-реакции
,Proc. Рой. соц. Лонд.
, стр.271
–281
.,
2002
.Разрывный пространственно-временной метод Галеркина с динамическим движением сетки для невязких сжимаемых течений: I. Общая формулировка
,J. Comput. физ.
,182
(2
),546
–585
.,
1984
. .,
1986
. .© 2007 Автор Сборник журнала © 2007 РАН
Произошла ошибка при настройке пользовательского файла cookie
Произошла ошибка при настройке пользовательского файла cookie Этот сайт использует файлы cookie для повышения производительности.Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.
Настройка браузера на прием файлов cookie
Существует множество причин, по которым файл cookie не может быть установлен правильно. Ниже приведены наиболее распространенные причины:
- В вашем браузере отключены файлы cookie. Вам необходимо сбросить настройки браузера, чтобы принять файлы cookie, или спросить вас, хотите ли вы принимать файлы cookie.
- Ваш браузер спрашивает, хотите ли вы принимать файлы cookie, и вы отказались.Чтобы принять файлы cookie с этого сайта, нажмите кнопку «Назад» и примите файл cookie.
- Ваш браузер не поддерживает файлы cookie. Попробуйте другой браузер, если вы подозреваете это.
- Дата на вашем компьютере в прошлом. Если часы вашего компьютера показывают дату до 1 января 1970 г., браузер автоматически забудет файл cookie. Чтобы это исправить, установите правильное время и дату на своем компьютере.
- Вы установили приложение, которое отслеживает или блокирует установку файлов cookie.
 Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.
Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.
Почему этому сайту требуются файлы cookie?
Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу. Предоставить доступ без файлов cookie потребует от сайта создания нового сеанса для каждой посещаемой вами страницы, что замедляет работу системы до неприемлемого уровня.
Что сохраняется в файле cookie?
Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в файле cookie; никакая другая информация не фиксируется.
Как правило, в файле cookie может храниться только та информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта. Например, сайт
не может определить ваше имя электронной почты, если вы не решите ввести его. Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступ к
остальной части вашего компьютера, и только сайт, создавший файл cookie, может его прочитать.
Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступ к
остальной части вашего компьютера, и только сайт, создавший файл cookie, может его прочитать.
%PDF-1.4
5 0 объект
>
эндообъект
8 0 объект
(БЛАГОДАРНОСТИ)
эндообъект
9 0 объект
>
эндообъект
12 0 объект
(СПИСОК ТАБЛИЦ)
эндообъект
13 0 объект
>
эндообъект
16 0 объект
(СПИСОК РИСУНКОВ)
эндообъект
17 0 объект
>
эндообъект
20 0 объект
(АННОТАЦИЯ)
эндообъект
21 0 объект
>
эндообъект
24 0 объект
(ВВЕДЕНИЕ)
эндообъект
25 0 объект
>
эндообъект
28 0 объект
(Введение в проблему)
эндообъект
29 0 объект
>
эндообъект
32 0 объект
(Обработка и процесс удаления материала)
эндообъект
33 0 объект
>
эндообъект
36 0 объект
(Применение в промышленности)
эндообъект
37 0 объект
>
эндообъект
40 0 объект
(Литературное исследование)
эндообъект
41 0 объект
>
эндообъект
44 0 объект
(ЭКСПЕРИМЕНТАЛЬНАЯ МОДАЛЬНАЯ ПРОВЕРКА)
эндообъект
45 0 объект
>
эндообъект
48 0 объект
(Динамический отклик линейных систем)
эндообъект
49 0 объект
>
эндообъект
52 0 объект
(Обзор ударных испытаний)
эндообъект
53 0 объект
>
эндообъект
56 0 объект
(Эффекты нагрузки контактного датчика)
эндообъект
57 0 объект
>
эндообъект
60 0 объект
(ПРОГНОЗ ДИНАМИЧЕСКОГО ОТКЛИКА НЕПРЕРЫВНЫХ ЛУЧЕЙ)
эндообъект
61 0 объект
>
эндообъект
64 0 объект
(Вывод уравнения движения)
эндообъект
65 0 объект
>
эндообъект
68 0 объект
(Прогноз динамического отклика однородных лучей)
эндообъект
69 0 объект
>
эндообъект
72 0 объект
(Экспериментальный ответ однородных лучей)
эндообъект
73 0 объект
>
эндообъект
76 0 объект
(ПРОГНОЗ ДИНАМИЧЕСКОГО ОТКЛИКА РАЗРЫВНЫХ ПУЧКОВ)
эндообъект
77 0 объект
>
эндообъект
80 0 объект
(Вывод приемной способности для прерывистых балок с выровненными нейтральными осями)
эндообъект
81 0 объект
>
эндообъект
84 0 объект
(Решение с прерывистым ступенчатым пучком для силового возбуждения в точке C)
эндообъект
85 0 объект
>
эндообъект
88 0 объект
(Решение с прерывистым ступенчатым пучком для силового возбуждения в точке A)
эндообъект
89 0 объект
>
эндообъект
92 0 объект
(Расширение аналитического решения для прикладных пар)
эндообъект
93 0 объект
>
эндообъект
96 0 объект
(Сравнение аналитического решения с реактивной связью)
эндообъект
97 0 объект
>
эндообъект
100 0 объект
(Экспериментальная проверка решения для ступенчатой балки)
эндообъект
101 0 объект
>
эндообъект
104 0 объект
(Вывод приемной способности для прерывистых балок со смещенными нейтральными осями)
эндообъект
105 0 объект
>
эндообъект
108 0 объект
(Решение с прерывистым смещенным пучком для силового возбуждения в точке C)
эндообъект
109 0 объект
>
эндообъект
112 0 объект
(Экспериментальное исследование решения смещенной нейтральной оси)
эндообъект
113 0 объект
>
эндообъект
116 0 объект
(УСТОЙЧИВОСТЬ ПРОЦЕССА СНЯТИЯ СЛОЯ)
эндообъект
117 0 объект
>
эндообъект
120 0 объект
(Ограничение ширины стружки для процесса обработки)
эндообъект
121 0 объект
>
эндообъект
124 0 объект
(Анализ формы моды как функция высоты выреза)
эндообъект
125 0 объект
>
эндообъект
128 0 объект
(ВЫВОДЫ И ДАЛЬНЕЙШАЯ РАБОТА)
эндообъект
129 0 объект
>
эндообъект
132 0 объект
(ИСПОЛЬЗОВАННАЯ ЛИТЕРАТУРА)
эндообъект
133 0 объект
>
эндообъект
136 0 объект
(БИОГРАФИЧЕСКИЙ ОЧЕРК)
эндообъект
137 0 объект
>
эндообъект
140 0 объект >
ручей
xڍSn0+xb|ґ)D9″rjўe’A}A@$|H͵I➵AB|`ֱc;|B8×D &R6tƑZj*Uꆅxu. Pfb?dmKfaZ*ve-Υhï ϏX|f?TWWm+g0_嚲@d\
Pfb?dmKfaZ*ve-Υhï ϏX|f?TWWm+g0_嚲@d\
Анализ разрывных деформаций в практике механики горных пород
Содержание
Введение
1.1 Кому следует прочитать эту книгу?
1.2 Как пользоваться этой книгой?
1.3 Непрерывная и прерывистая деформации
1.4 История МДД
1.5 Три десятилетия исследований и разработок МДД
1.6 МДД по сравнению с МКЭ и ЦМР
1.7 Основные характеристики МДД
1.8 Некоторые ограничения оригинального МДД
1.9 Блочная дискретизация
1.10 Функция смещения высшего порядка
1.11 Сочетание DDA с другими численными методами
1.12 Улучшенные контактные алгоритмы
1.13 Включение вязкостного демпфирования
1.14 Улучшенный закон трения для несплошностей
1.15 Включение гравитации и последовательная экскавация
1.16 Динамическое распространение волн и взрывные работы
1.16 Динамическое распространение волн и взрывные работы
1.16
1.18 Усовершенствованный элемент анкера
1. 19 Гранулированные материалы
19 Гранулированные материалы
1.20 Поровое давление и поток жидкости
1.21 Текущая разработка 3-D DDA
2 Теория анализа прерывистых деформаций (DDA)
2.1 Основные уравнения и аппроксимация смещения
2.2 Формулировка матриц для каждого отдельного блока
2.3 Взаимодействие между блоками
2.4 Схема интегрирования по времени и основные уравнения для блочных систем
2.5 Симплексное интегрирование для 2-D DDA
2.6 Резюме
3 Теория анализ прерывистой деформации в трех измерениях
3.1 Аппроксимация смещения блока и уравнение глобального равновесия
3.2 Формулировка матриц для отдельного блока
3.3 Взаимодействие между блоками
3.4 Симплексная интеграция для 3D DDA
3.5 Резюме
4 Геологические входные параметры для реалистичного DDA-моделирования
4.1 Введение
4.2 Реалистическое представление структуры горного массива
4.3 Механические входные параметры для прямого моделирования
5.
 1 Введение
1 Введение 5.2 Скольжение в одной плоскости
5.3 Скольжение в двух плоскостях
5.4 Реакция блока на циклическое движение фрикционного интерфейса
5.5 динамических качания стройных блоков
5.6 0,6 явления распространения волн
6 подземных раскопок 6.1 Введение
6.2 Глубокие подземные раскопки
6.3 Глубокие подземные раскопки
7 Rock Scores
7.1 Введение
7.2 Режимы отказа вращения
7.3 динамический анализ устойчивости откосов
7.4 Армирование анкерными болтами
8 Новая контактная теория Ши
8.1 Введение
8.2 Геометрические представления углов и блоков
8.3 Определение входного блока
8.4 Основные теоремы входного блока
8.5 Границы входных телесных углов 2D телесных углов
8.6 Контактные векторы 2D телесных углов
8.7 Границы входного блока 2D блоки
8.8 Контактные ребра 2D блоков
8.9 Границы входного телесного угла 3D телесного угла
8.

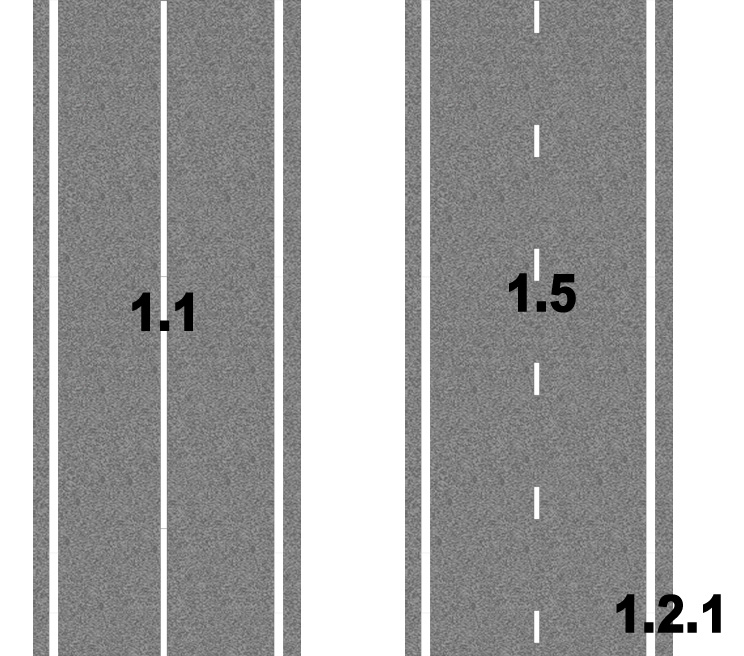

 Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.
Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.